next up previous
Next: Zahlentheoretische Grundlagen Up: Division nach Beame, Cook Previous: Division mittels Inversenbildung in NC 1

Inversenbildung durch geometrische Reihe in NC 1

Annahme:

Es stehen NC 1-Schaltkreise zur Verfügung, die $\varepsilon^{i}_{}$ ( 0 $\leq$ $\varepsilon$ < 1 , 0 $\leq$ i < n ) berechnen.
Dann ist folgender Algorithmus zur Berechnung von z : = $ \mathop {\rm inverse} $(y,n) in NC 1und korrekt (sei y > 0): 

 AC 0 $\qquad$   k : = |y|  
 AC 0		      

 $\varepsilon$ : = 1 - y $\cdot$ 2- k 
 NC 1		      berechne 

 $\varepsilon^{i}_{}$  für 

 i = 0,1,...,n - 1  parallel 
 NC 1		      

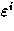
 z : = 2- k$\sum_{i=0}^{n-1}$$\varepsilon^{i}_{}$

Beweis:

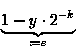Zu zeigen ist 0 $\leq$ ${\frac{1}{y}}$ - $ \mathop {\rm inverse} $(y,n) $\leq$ ${\frac{1}{y \cdot 2^n}}$ . Gesetzt ist k = |y| , d.h. 2k - 1 $\leq$ y < 2k $\Longleftrightarrow$ 2- 1 $\leq$ y $\cdot$ 2- k < 20 $\Longleftrightarrow$ ${\frac{1}{2}}$ $\geq$ $\underbrace{1 - y \cdot 2^{-k}}_{:= \varepsilon}^{}$ > 0. Also können wir die geometrische Reihe wie folgt anwenden:
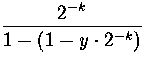$\displaystyle{\textstyle\frac{1}{y}}$ = $\displaystyle{\frac{2^{-k}}{y \cdot 2^{-k}}}$ = $\displaystyle{\frac{2^{-k}}{1-(1-y\cdot 2^{-k})}}$ = 2- k$\displaystyle{\textstyle\frac{1}{1-\varepsilon}}$ =   
  = 2- k$\displaystyle\sum_{i=0}^{\infty}$$\displaystyle\varepsilon^{i}_{}$ = 2- k($\displaystyle\sum_{i=0}^{n-1}$$\displaystyle\varepsilon^{i}_{}$ + $\displaystyle\varepsilon^{n}_{}$$\displaystyle\sum_{i=0}^{\infty}$$\displaystyle\varepsilon^{i}_{}$)   
  = 2- k($\displaystyle\sum_{i=0}^{n-1}$$\displaystyle\varepsilon^{i}_{}$ + $\displaystyle{\frac{\varepsilon^n}{1-\varepsilon}}$)   

Mit $ \mathop {\rm inverse} $(y,n) = 2- k$\sum_{i=0}^{n-1}$$\varepsilon^{i}_{}$ erhalten wir

d : = $\displaystyle{\textstyle\frac{1}{y}}$ - $\displaystyle \mathop {\rm inverse} $(y,n) = $\displaystyle{\frac{2^{-k}}{1-\varepsilon}}$$\displaystyle\varepsilon^{n}_{}$ = $\displaystyle{\textstyle\frac{1}{y}}$$\displaystyle\varepsilon^{n}_{}$,

denn 1 - y $\cdot$ 2- k = $\varepsilon$ $\Longleftrightarrow$ 1 - $\varepsilon$ = y $\cdot$ 2- k $\Longleftrightarrow$ 2k(1 - $\varepsilon$) = y $\Longleftrightarrow$ ${\frac{2^{-k}}{1-\varepsilon}}$ = ${\frac{1}{y}}$ , und wegen $\varepsilon$ $\leq$ ${\frac{1}{2}}$ gilt ( d $\geq$ 0 klar)

0 $\displaystyle\leq$ d $\displaystyle\leq$ $\displaystyle{\textstyle\frac{1}{y\cdot 2^n}}$.

Die Berechnung einer Potenz $\varepsilon^{n}_{}$ lässt sich auf die Berechnung des Produkts $\prod_{i=1}^{n}$xi von n natürlichen Zahlen x1,...,xn zurückführen. Der naheliegendste Algorithmus dafür ist aber in NC 2. Idee für einen NC 1-Algorithmus:

log($\displaystyle\prod_{i=1}^{n}$xi) = $\displaystyle\sum_{i=1}^{n}$(logxi)

Zurückführung auf eine Summe von Logarithmen. Da wir nur Ganzzahl-Arithmetik zur Verfügung haben, benötigen wir den diskreten Logarithmus.

next up previous
Next: Zahlentheoretische Grundlagen Up: Division nach Beame, Cook Previous: Division mittels Inversenbildung in NC 1
Andreas Abel
12/10/1997