Sing Bing Kang,
Jon A. Webb,
C. Lawrence Zitnick, and
Takeo Kanade
This paper will appear in the proceedings of the International
Conference on Computer Vision, Cambridge, MA, 1995.
Table of Contents
Abstract
We describe our implementation of a parallel depth recovery scheme for a four-camera multibaseline stereo in a convergent configuration. Our system is capable of image capture at video rate. This is critical in applications that require three-dimensional tracking. We obtain dense stereo depth data by projecting a light pattern of frequency modulated sinusoidally varying intensity onto the scene, thus increasing the local discriminability at each pixel and facilitating matches. In addition, we make most of the camera view areas by converging them at a volume of interest. Results show that we are able to extract stereo depth data that are, on the average, less than 1 mm in error at distances between 1.5 to 3.5 m away from the cameras.
Binocular stereo vision is a simple and flexible method by which three-dimensional (range) information of a scene can be obtained. Therefore, it is not surprising to find that stereo is a very active area of research [2]. The geometrical issues in stereo have also been well explored [6]. The primary drawback of stereo is the problem with image point correspondence (for a survey of correspondence techniques, see [5]). The trade-off between accuracy (which is aided by a wide baseline, or separation between the cameras) and ease of correspondence (which is simpler with a narrow baseline) has been mitigated using multiple cameras or camera locations. Such an approach has been termed multibaseline stereo [13].
Stereo vision is computationally intensive. Fortunately, the spatially repetitive nature of depth recovery lends itself to parallelization. A number of researchers have worked on fast implementation of stereo (e.g., [12], [14], [15]).
In this paper, we describe our implementation of a depth recovery scheme implemented in iWarp for a four-camera multibaseline stereo in a convergent configuration. Our system is capable of image capture at video rate. This is critical in applications that require tracking in three dimensions (an example is [10]). One method to obtain dense stereo depth data is to interpolate between reliable pixel matches [8]. However, the interpolated values may not be accurate. We obtain accurate dense depth data by projecting a light pattern of sinusoidally varying intensity onto the scene, thus increasing the local discriminability at each pixel. In addition, we make the most of the camera view areas by converging them at a volume of interest. Experiments have indicated that we are able to extract stereo depth data that are, on the average, less than 1 mm in error at distances between 1.5 to 3.5 m away from the cameras.
Our multibaseline camera system is shown in Fig. 1. It comprises four cameras mounted on a metal bar, which in turn is mounted on a sturdy tripod stand; each camera can be rotated about a vertical axis and fixed at discrete positions along the bar. The four camera video signals are all synchronized by ganging the genlock signals.

In addition to the camera, we use a projector to cast a pattern of sinusoidal varying intensity (active lighting) onto the scene. This notion of a multibaseline stereo with active illumination allows a denser depth map as a result of improved local scene discrimination and hence correspondence.
The primary problem associated with a stereo arrangement of parallel camera locations is the limited overlap between the fields of views of all the cameras. The percentage of overlap increases with depth. The primary advantage is the simple and direct formula in extracting depth.
Verging the cameras at a specific volume in space is optimal in an indoor application where maximum utility of the camera visual range is desired and the workspace size is constrained and known a priori. One such application is the tracking of objects in the Assembly Plan from Observation project [9][10].
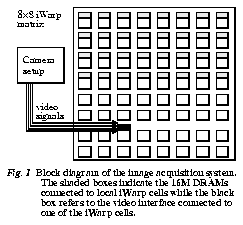
Our image acquisition system consists of the physical camera setup described earlier in this section, the video interface board, and the 8×8 matrix of iWarp cells (Fig. 2). Each iWarp component contains a 20 MFLOPS computation engine and low-latency (100-150 ns) communication engine for interfacing with other iWarp cells [3]. The existing iWarp system is an 8×8 torus of iWarp cells, half of which have 16 MB DRAMS per cell. The video interface, which is described in detail elsewhere [18], is connected directly to the iWarp cell through the memory interface; the digitized video data is routed and distributed at video rate to the DRAMs by taking advantage of iWarp's systolic design [4].
Before data images can be taken and the scene depth recovered, we must first calibrate the camera configuration. Calibrating the camera configuration refers to the determination of the extrinsic (relative pose) and intrinsic (optic center offset, focal length and aspect ratio) camera parameters. The pinhole camera model is assumed in the calibration process. The origin of the verged camera configuration coincides with that of the leftmost camera.
Calibration is done by detecting dot patterns at several known depths and using the non-linear least-squares technique described by Szeliski and Kang [17]. An alternative would be to use the pairwise-stereo calibration approach proposed by Faugeras and Toscani [7].
If two camera axes are not parallel, their associated epipolar lines are not parallel to the scan lines. To simplify and reduce the amount of depth-from-stereo computation, rectification can be carried out first. The process of rectification for a pair of images transforms the original pair of image planes to another pair such that the resulting epipolar lines are parallel and equal along the new scan lines. Rectification is depicted in Fig. 3. Here c1 and c2 are the camera optical centers, Π1 and Π2 the original image planes, and Ω1 and Ω2 the rectified image planes. The condition of parallel and equal epipolar lines necessitates planes Ω1 and Ω2 to lie in the same plane, indicated as Ω12. A point q is projected to image points v1 and v2 on the same scan line in the rectified planes.

A simple rectification method is described in [1]. However, the rectification process described there is a direct function of the locations of the camera optical centers. We have modified their formalism to simplify the rectification mapping and adapt it to our situation. We choose the common rectified camera axis direction to be midway between those of the unrectified camera axes. Details of our image rectification scheme can be found in [11].
There are two schemes which allows us to recover depth. The first uses all the homographies (or linear projective correspondences) between the unrectified images and rectified images (namely H11, H12, H13, H21, H32, and H43 in Fig. 4).

Subsequent to rectification, to recover depth, we first determine the corresponding location in the rectified image plane for the three pairs of cameras (Fig. 4). We wish to recover the 3D location q of the image point corresponding to u0. q can be specified in the following form:
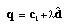
where c1 is the optical center of the first ("reference") camera,  is the unit vector in the direction from c1 to q, and λ is the depth of q from the reference camera optical center. If
is the unit vector in the direction from c1 to q, and λ is the depth of q from the reference camera optical center. If

where 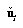 ,
,  and
and  follow the notation in Fig. 4 with the ~ indicating homogeneous representation, then the disparity Δj can be found to be ([11])
follow the notation in Fig. 4 with the ~ indicating homogeneous representation, then the disparity Δj can be found to be ([11])

where
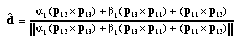
By varying λ within a specified interval and resolution, we can calculate Δj's for the pairs of rectified images, and hence calculate the sum of matching errors (as in [13] with multiple parallel cameras). The depth is recovered by picking the value of λ associated with the least matching error.
The method described above implies that we must calculate, at each point and for each depth, the corresponding points in all images. This requires projective transformations of all images to be performed for each depth value. There is a more computationally efficient way to recover depth. This stems from the following properties:
1. The two rectified planes fall on the same plane.
2. The line joining the two projection centers is parallel to this common plane.
Properties 1 & 2 (which are the necessary conditions for rectification) give rise to
3. The homography between the two rectified planes cannot be projective (since the scan lines on the rectified images are parallel, i.e., the corresponding rows at both rectified images are equal). This is true since the "projection" lines (the corresponding scan lines) meet at infinity.
From 3, the homography between rectified planes must then be at most a 2D affine transform, i.e., the last row of the homography matrix must be (0 0 1). This dispenses with the additional division by the z-component in calculating the corresponding matched point for a particular depth.
The scheme now follows that in Fig. 5. The matching is done using the homographies between rectified images K1, K2 and K3 (which we term rectified homographies). The rectified homographies can be readily determined as follows:
For a known depth plane (z = d), we can "contract" the 3×4 perspective matrix M (to the rectified plane) to a 3×3 homography G. For camera l, we have
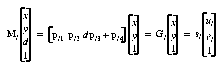
where plj is the jth column of Ml and (ul, vl)T is the projected image point in camera l. Similarly, for camera m,
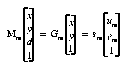
Since the rectified planes are coplanar, sl = sm; hence
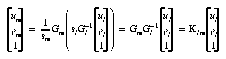
Note that, due to rectification, vm = vl, and as explained earlier in this subsection, the bottom row of Klm is (0 0 1). In other words, the projective transformations are reduced to affine transformations, reducing the amount of computation.

Depth recovery then proceeds in a similar manner as the direct approach described in the previous subsection.
In both approaches described earlier, for each depth, each pixel in the unrectified reference image has to be mapped Ncameras--1 times to the respective rectified images (corresponding to the homographies H11, H12, and H13 in Fig. 5). We can work in the rectified image coordinates (say M1), but this still requires mapping from M2 to M1 and M3 to M1 in the collection of match errors for each depth value. This means that we need to perform (Ncameras--2)Ndepth sets of bilinear interpolations associated with image warping (where Ndepth is the number of depth values and Ncameras is the number of cameras).
In order to avoid the warping operations, we use an approximate depth recovery method. The matching is done with respect to the rectified image of the first pair. However, the rectified images N2 and N3 will not be row preserved relative to M1 (Fig. 6). We warp rectified images N2 and N3 so as to preserve the rows as much as possible, resulting in N'2 and N'3 (Fig. 6). The errors should be tolerably small as long as the vergence angles are small. In addition, this effect should not pose a significant problem as we are using a local windowing technique in calculating the match error.
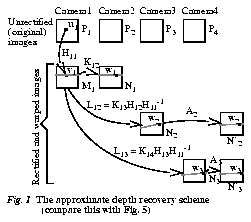
By comparing Fig. 6 with Fig. 5, we can see that the mapping from M1 to N2 is given by the homography L12 = K13H12H11-1. Similarly, the mapping from M1 to N3 is given by L13 = K14H13H11-1. The matrices A2 and A3 are constructed such that

i.e., the resulting overall mapping is row preserving (r and c are the row and column respectively). In general, this would not be possible, unless all the camera centers are colinear; however, this is a good approximation for small vergence angles and approximately aligned cameras. A2 and A3 are calculated from the following overconstrained relation using the pseudoinverse calculation:

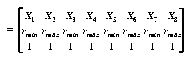
where 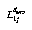 is associated with the minimum depth and
is associated with the minimum depth and  with the maximum depth, cmin and cmax are the minimum and maximum values of the image column, and rmin and rmax are the minimum and maximum values of the image row, respectively. Xi (i=1,...,8) are don't-care values. The symbol | is used to represent matrix augmentation.
with the maximum depth, cmin and cmax are the minimum and maximum values of the image column, and rmin and rmax are the minimum and maximum values of the image row, respectively. Xi (i=1,...,8) are don't-care values. The symbol | is used to represent matrix augmentation.
This algorithm has been implemented in parallel using the Fx (parallel Fortran) language developed at Carnegie Mellon [16]. Fx, a variant of High Performance Fortran with optimizations for high-communication applications like signal and image processing, runs on the Carnegie Mellon-Intel Corporation iWarp, the Paragon/XPS, the Cray T3D, and the IBM SP2. The experiments reported in this paper were done on the iWarp.
In this section, we present results of our active multibaseline stereo system. As mentioned before, a pattern of sinusoidally varying intensity are projected onto the scenes to facilitate image point correspondence.
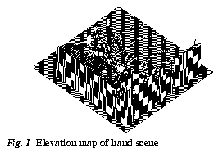
An example (hand scene) is shown in Fig. 7 with the recovered elevation map in Fig. 8. As can be seen from the elevation map, except at the edges of the objects on the scene, the data looks very reasonable. The large peaks at the borders of the depth map are outliers due to mismatches in the background outside the depth range of interest.

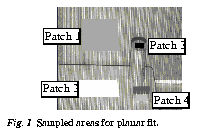
We have also performed some error analysis on some of the range data that were extracted from another scene. Fig. 9 show the areas for planar fit; Table 1 shows the numerical results of the planar fit. As can be seen, the average planar fit error is smaller than 1 mm (the furthest planar patch is about 1.7m away from the camera system).
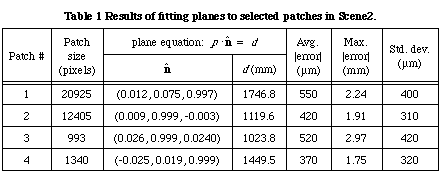
We have also obtained stereo range data of a cylinder of known cross-sectional radius and calculated the fit error. In both scenes (with different camera settings), the cylinder is placed about 3.3 m away from the camera system.

As can be seen from Table 2, the mean absolute error of fit is less than 1 mm.

We have achieved better than 1mm accuracy. The sources of error in our system and in stereo generally include:
1. The use of multibaseline stereo with active illumination reduces the chance of false matches, but they can still occur.
2. The fundamental assumptions of stereo are that the texture being viewed is unique over the search window, and that the surface is visible to and lies at the same angle to all camera optical axes. The former assumption is addressed by the active component of our system, but the latter is not and cannot be, except by placing the cameras as close together as possible (which reduces accuracy). The failure of this assumption is particularly evident at the boundaries of objects, where it is the cause of significant error.
3. Calibration errors occur due to uncertainty in positioning our calibration plate and locating the dot pattern positions.
4. We use a pinhole camera model, which is not exact.
5. We make the approximation discussed in Section 4.3, which will result in errors when the camera optical centers are not colinear.
Of these, the first seems to be a cause of significant error. All of the large errors (> 1 mm) are observed to be in regions where the projected pattern does not provide sufficient texture for a correct match.
We have attempted to reduce these errors by analysis and experimentation. Analysis shows that a frequency-modulated sine wave pattern, as used there, is a good choice since it does not require large dynamic range. Also, a randomly frequency-modulated sine wave gives the best possible result, since the same pattern occurs twice in the search area with vanishingly small probability, theoretically eliminating the possibility of false matches. Experiments with randomly modulated patterns have shown that
- The lowest observed frequency of the sine wave must be higher than the width of the correlation match window.
- The highest frequency usable is constrained by the resolution of the camera and the focus control of the projector. Using a higher frequency than the maximum results in a gray blur and many false matches.
The trade-off between these two constraints involves optimizing the projector placement and focus, the camera resolution, the number of cameras, and the camera dynamic range.
In addition, many of the problems of false matches occur where the limited dynamic range of our video interface plays a role, particularly with dark surfaces or sufaces which lie almost parallel to the projection, or surfaces with specularities. The use of multiple projectors/patterns, either time-sequenced or color-sequenced (using color cameras) may serve to reduce these effects.
We have briefly described a 4-camera system that is capable of video rate image acquisition. It uses a software distribution approach which takes advantage of iWarp's systolic design. The four cameras are used in a converging configuration for more effective use of the camera view spaces. In addition, to recover dense stereo range data from each set of images, we project a sinusoidally varying pattern onto the scene to enhance local intensity discriminability. This results in a multibaseline stereo system with active illumination.
We have also described in detail our implementation of the depth recovery algorithm which involves the preprocessing stage of image rectification. Our approximate depth recovery implementation was designed for reduced computation.
The results that we have obtained from this system indicated that the mean errors (discounting object border areas) are less than a millimeter at distances varying from 1.5 m to 3.5 m from the camera system. The performance of the system is thus comparable to a good structured light system, while allowing data to be captured at full video rate.
Acknowledgments
Many thanks to Bill Ross for his helpful information on setting up a multibaseline camera system. Tom Warfel built the real-time video interface board to the iWarp that made this project possible. We are also grateful to Luc Robert for interesting discussions on image rectification. Mark Wheeler helped in the analysis that led to the decision to verge the cameras.
References
[1] Ayache, N. and C. Hansen. Rectification of images for binocular and trinocular stereovision. in Proc. of the 9th Int'l Conf. on Patt. Recog. 1988. Rome, Italy.: p. 11-16.
[2] Barnard, S.T. and M.A. Fischler, Computational stereo. Computing Surveys, 1982. 14(4): p. 554-572.
[3] Borkar, S., et al. iWarp: An Integrated Solution to High-Speed Parallel Computing. in Proc. of Supercomputing '88. 1988. Orlando, Florida.: p. 330-339.
[4] Borkar, S., et al. Supporting Systolic and Memory Communication in iWarp. in Proc. of the 17th Int'l Symp. on Computer Architecture. 1990. Seattle, WA.: p. 70-81.
[5] Dhond, U.R. and J.K. Aggarwal, Structure from stereo - A review. IEEE Trans. on Systems, Man, and Cybernetics, 1989. 19(6): p. 1489-1510.
[6] Faugeras, O.D., Three-Dimensional Computer Vision: A Geometric Viewpoint. 1993, MIT Press.
[7] Faugeras, O.D. and G. Toscani. The calibration problem for stereo. in Proc. of the IEEE Int'l Conf. on Computer Vision and Patt. Recog. 1986: p. 15-20.
[8] Fua, P., A parallel stereo algorithm that produces dense depth maps and preserves image features. Machine Vision and Applications, 1993. 6: p. 35-49.
[9] Ikeuchi, K. and T. Suehiro. Towards an Assembly Plan from Observation. in Proc. of the IEEE Int'l Conf. on Robotics and Automation. 1992: p. 2171-2177.
[10] Kang, S.B. and K. Ikeuchi. A robot system that observes and replicates grasping tasks. in Proc. of Int'l Conf. on Computer Vision. 1995.
[11] Kang, S.B., J.A. Webb, C.L. Zitnick and T. Kanade. An active multibaseline stereo system with real-time acquisition. in Proc. Image Understanding Workshop. Monterey, CA. Nov. 1994. p. 1325-1334.
[12] Matthies, L., Stereo vision for planetary rovers: Stochasting modeling to near real-time implementation. Int'l Journal of Computer Vision, 1992. 8(1): p. 71-91.
[13] Okutomi, M. and T. Kanade, A Multiple-Baseline Stereo. IEEE Trans. on PAMI, 1993. 15(4): p. 353-63.
[14] Ross, B. A practical stereo vision system. in Proc. of the IEEE Int'l Conf. on Computer Vision and Patt. Recog. 1993: p. 148-153
[15] Rygol, M., et al., A Parallel 3D Vision System, in Active Vision, A. Blake and A. Yuille, Editors. 1992, MIT Press: Cambridge, MA. p. 239-261.
[16] Subhlok, J., et al. Exploiting Task and Data Parallelism on a Multicomputer. in Symp. on Principles and Practice of Parallel Programming. 1993: ACM SIGPLAN.
[17] Szeliski, R. and S.B. Kang, Recovering 3D shape and motion from image streams using non-linear least squares. J. of Visual Comm. and Image Rep., 1994. 5(1): p. 10-28.
[18] Webb, J.A., T. Warfel, and S.B. Kang, A Scalable Video Rate Camera Interface. Tech. Rep. CMU-CS-94-166, Computer Science Dept., Carnegie Mellon Univ., 1994.
[19] Wheeler, M.D. and K. Ikeuchi, Sensor modeling, probabilistic hypothesis generation, and robust localization for object recognition. in Proc. of the 2nd CAD-Based Vision Workshop, 1994: p. 46-53.


 is the unit vector in the direction from c1 to q, and λ is the depth of q from the reference camera optical center. If
is the unit vector in the direction from c1 to q, and λ is the depth of q from the reference camera optical center. If 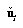 ,
,  and
and  follow the notation in Fig. 4 with the ~ indicating homogeneous representation, then the disparity Δj can be found to be ([11])
follow the notation in Fig. 4 with the ~ indicating homogeneous representation, then the disparity Δj can be found to be ([11])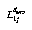 is associated with the minimum depth and
is associated with the minimum depth and  with the maximum depth, cmin and cmax are the minimum and maximum values of the image column, and rmin and rmax are the minimum and maximum values of the image row, respectively. Xi (i=1,...,8) are don't-care values. The symbol | is used to represent matrix augmentation.
with the maximum depth, cmin and cmax are the minimum and maximum values of the image column, and rmin and rmax are the minimum and maximum values of the image row, respectively. Xi (i=1,...,8) are don't-care values. The symbol | is used to represent matrix augmentation.