We begin by specifying a large collection 
of candidate features. We do
not require a priori that these features are actually relevant or useful.
Instead, we let the pool be as large as practically possible. Only a small
subset of this collection of features will eventually be employed in our final
model. In short, we would like to include in the model only a subset 
of
the full set of candidate features 
. We will call 
the set of
active features. The choice of 
must capture as much information about
the random process as possible, yet only include features whose expected values
can be reliably estimated.
With each 
one might associate a Bernoulli random variable 
with the following (``objectivist'' or ``non-Bayesian'')
interpretation. Imagine that the set of 
pairs comprising 
were
drawn from an imaginary, infinite distribution of 
pairs. In this imaginary
distribution, f is active ( 
) with some probability 
, and
inactive ( 
) with probability 
.
(A Bayesian would prefer to put a distribution over the possible values of
, informed both by some empirical evidence--such as the fraction of
times 
in the sample 
--and also by some outside knowledge of
what one miht expect 
to be. This line of reasoning forms the basis of
``fuzzy maximum entropy,'' which is a quite intriguing line of investigation we
shall not pursue here.)
As a Bernoulli variable, f is subject to the law of large
numbers,
which asserts that for
any 
:
That is, by increasing the number (N) of examples 
, the fraction
for which 
approaches the constant 
. More
succinctly, 
.
Unfortunately, 
is not infinite, and the empirical estimate
for each 
is not guaranteed to lie close to its ``true'' value
. However, a subset of 
will exhibit 
. And of these, a fraction will have a non-negligeable bearing on the
likelihood of the model. The goal of the inductive learning process is to identify
this subset and construct a conditional model from it.
Searching exhaustively for this subset is hopeless for all but the most
restricted problems. Even a priori fixing its size 
doesn't
help much: there are 
unique outcomes
of this selection process. For concreteness, a typical set of figures in
documented experiments involving maxent modeling are 
and 
, meaning 
possible sets of 25 active
features. Viewed as a pure search problem, finding the optimal set of
features is computationally inconceivable.
To find 
, we adopt an incremental approach to feature selection. The idea
is to build up 
by successively adding features. The choice of feature to
add at each step is determined by the training data. Let us denote the set of
models determined by the feature set 
as 
. ``Adding'' a feature f
is shorthand for requiring that the set of allowable models all satisfy the
equality 
. Only some members of 
will satisfy this
equality; the ones that do we denote by 
.
Thus, each time a candidate feature is adjoined to 
, another linear
constraint is imposed on the space 
of models allowed by the features
in 
. As a result, 
shrinks; the model 
in 
with the
greatest entropy reflects ever-increasing knowledge and thus, hopefully,
becomes a more accurate representation of the process. This narrowing of the
space of permissible models was represented in figure 1 by a
series of intersecting lines (hyperplanes, in general) in a probability
simplex. Perhaps more intuitively, we could represent it by a series of nested
subsets of 
, as in figure 2.
As an aside, the intractability of the ``all at once'' optimization problem is not unique to or an indictment of the exponential approach. Decision trees, for example, are typically constructed recursively using a greedy algorithm. And in designing a neural network representation of an arbitrary distribution, one typically either fixes the network topology in advance or performs a restricted search within a neighborhood of possible topologies for the optimal configuration, because the complete search over parameters and topologies is intractable.
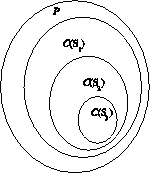
Figure 2: A nested sequence of
subsets 
of 
corresponding to increasingly large sets of features 
