Primes

   

Our second example finds all the primes less than n. The algorithm is based on the sieve of Eratosthenes. The basic idea of the sieve is to find all the primes less than , and then use multiples of these primes to ``sieve out'' all the composite numbers less than n. Since all composite numbers less than n must have a divisor less than , the only elements left unsieved will be the primes. There are many parallel versions of the prime sieve, and several naive versions require a total of work and either or parallel time. A well designed version should require no more work than the serial sieve ( ), and polylogarithmic parallel time.

  
Figure: Finding all the primes less than n.

The version we use (see Figure 7) requires work and depth. It works by first recursively finding all the primes up to , (sqr_primes). Then, for each prime p in sqr_primes, the algorithm generates all the multiples of p up to n (sieves). This is done with the [s:e:d] construct. The sequence sieves is therefore a nested sequence with each subsequence being the sieve for one of the primes in sqr_primes. The function flatten, is now used to flatten this nested sequence by one level, therefore returning a sequence containing all the sieves. For example,

This sequence of sieves is used by the <- function to place a false flag in all positions that are a multiple of one of the sqr_primes. This will return a boolean sequence, flags, which contains a t in all places that were not knocked out by a sieve--these are the primes. However, we want primes to return the indices of the primes instead of flags. To generate these indices the algorithm creates a sequences of all indices between 0 and n ([0:n]) and uses subselection to remove the nonprimes. The function drop is then used to remove the first two elements (0 and 1), which are not considered primes but do not get explicitly sieved.

The functions [s:e:d], flatten, dist, <- and drop all require a constant depth. Since primes is called recursively on a problem of size the total depth required by the algorithm can be written as the recurrence:

Almost all the work done by primes is done in the first call. In this first call, the work is proportional to the length of the sequence flat_sieves. Using the standard formula

where p are the primes [24], the length of this sequence is:

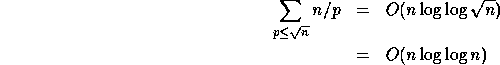
therefore giving a work complexity of .

  
Figure 8: An example of the quickhull algorithm. Each sequence shows one step of the algorithm. Since A and P are the two x extrema, the line AP is the original split line. J and N are the farthest points in each subspace from AP and are, therefore, used for the next level of splits. The values outside the brackets are hull points that have already been found.