Results

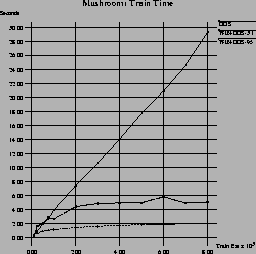
Figure 4 shows the accuracy, the number of processed examples, and the run-time results for the three algorithms in the Mushroom domain. WIN-DOS-3.1 seems to be effective in this domain, at least for larger training sets (> 1000). Our improved version, WIN-DOS-95, clearly outperforms simple windowing in terms of run-time, while there are no significant differences in terms of accuracy.

  

Figure 4: Results in the Mushroom domain.

In a typical run with the above-mentioned parameter settings, WIN-DOS-3.1 needs about 3 to 5 iterations for learning the correct concept, the last of them using a window size of about 200 to 350 examples. WIN-DOS-95 needs about the same number of iterations, but it rarely keeps more than 150 examples in its window. In total, WIN-DOS-3.1 submits about 1000 examples to the DOS learner, while WIN-DOS-95 can save about half of them. Figure 4 shows that these numbers remain almost constant after a saturation point of about 3,000 examples is reached, which is the point where all learners learn 100% correct theories. Learning from 500 to 1000 randomly selected examples does not result in correct theories, as can be inferred from the DOS accuracy curve. Thus, in this domain, a performance gain comparable to that achieved by windowing cannot be achieved with random sub-sampling. Hence we conclude that the systematic sub-sampling performed by windowing has its merits.

  

Figure 5: Results in the KRK, and KRKN domains.

Figure 5 shows the accuracy and run-time results for the three algorithms in the KRK and KRKN domains. The picture here is quite similar to Figure 4: WIN-DOS-3.1 seems to be effective in both domains, at least for larger training set sizes. Our improved version, WIN-DOS-95, clearly outperforms basic windowing in terms of run-time, while there are no significant differences in terms of accuracy. In the KRK domain, predictive accuracy reaches 100% at about 5000 training examples for all three algorithms. At lower training set sizes, WIN-DOS-95 is a little ahead, but in general there are no significant differences. The run-time of both windowing algorithms reaches a plateau at about the same size of 5000 training examples, which again shows that windowing does not use additional examples once it is able to discover a correct theory from a certain sample size.

The results in the KRKN chess endgame domain with training set sizes of up to 10,000 examples are quite similar. However, for smaller training set sizes, which presumably do not contain enough redundancy, basic windowing can take significantly longer than learning from the complete data set.

This behavior is more obvious in the results in the Tic-Tac-Toe endgame domain¹¹ shown in the top portion of Figure 6. Here, the predictive accuracy of all three algorithms reaches 100% at about half the total example set size. Interestingly, WIN-DOS-3.1 reaches this point considerably earlier (at about 250 examples). On the other hand, WIN-DOS-3.1 is not able to achieve an advantage over DOS in terms of run-time, although it seems quite likely that it would overtake DOS at slightly larger training set sizes. WIN-DOS-95 reaches this break-even point much earlier and continues to build up a significant gain in run-time at larger training set sizes.

  

Figure 6: Results in the Tic-Tac-Toe and KRKP domains.

In all domains considered so far, removing a few randomly chosen examples from the larger training sets did not affect the learned theories. Intuitively, we would call such training sets redundant as discussed in section 3.4. In the 3196 example KRKP data set, on the other hand, the algorithms are not able to learn theories that are 100% correct when tested on the complete data set unless they use the entire data set for training. Note that in this case the 100% accuracy estimate is in fact a re-substitution estimate, which may be a bad approximation for the true accuracy. We would call such a data set non-redundant, as it seems to be the case that randomly removing only a few examples will already affect the learned theories. In this domain, WIN-DOS-3.1 processes about twice as many examples as DOS for each training set size. Our improved version of windowing, on the other hand, processes only a few more examples than DOS at lower sizes, but seems to be able to exploit some redundancies of the domain at larger training set sizes. We interpret this a evidence for our hypothesis that even in non-redundant training sets, some parts of the example space may be redundant (section 3.4). This is consistent with previous findings, which showed that in this domain, a few accurate rules with high coverage can be found easily from small training sets, while the majority of the rules have low coverage and are very error-prone [34]. Interestingly enough, however, Møller's redundancy estimate, which seemed to correlate well with C4.5's performance in these domains in Table 2, is a poor predictor for the performance of our windowing algorithms. The KRKP set, which exhibits the worst performance and is not redundant according to our definition, has a much better redundancy estimate than the KRK data set, for which windowing works much better.

  

Figure 7: Results in the binarized Shuttle domain.

Figure 7 shows the results in the 43,500 examples Shuttle domain. For this domain, a separate test set is available (14,500 examples). The accuracy graphs show the performance of the algorithms on this test set. The upper half shows the results when training on the minority class (i.e., learning a theory for all examples with a non-1 classification). Both windowing algorithms perform exceptionally well in this domain, with WIN-DOS-95 being about twice as fast as WIN-DOS-3.1. In terms of accuracy, WIN-DOS-3.1 is more accurate than both other algorithms, WIN-DOS-95 being a little ahead of DOS. As this example set has a relatively skewed class distribution (about 80% of the examples are of class 1), we decided to also try the algorithms on the reverse problem by swapping the labels of the positive and negative examples. The results in terms of run-time did not change. However, in terms of accuracy, the performance of DOS improved, so that it equals WIN-DOS-3.1 with WIN-DOS-95 being behind both. We have not yet found a good explanation for this phenomenon.

It is interesting to note that this is the only domain we have tried that contains numeric attributes. We handled these in the common way using threshold tests. The candidate thresholds for each test are selected between changes in the class variables in the sorted list of values of the continuous attributes [23].¹² As the windowing algorithms will typically have to choose a threshold from a much smaller example set, they are likely to choose different thresholds. Whether this has a positive (less over-fitting), negative (the optimal threshold may be missed), or no effect at all is an open question, which has already been raised by [7] and has been further explored in Catlett's work on peepholing [11].

In summary, the results have shown us that significant run-time gains can be achieved with windowing (usually without losing accuracy), and even more so with integrative windowing in a variety of noise-free domains. However, we have also seen that redundancy is in fact a crucial condition for the effectiveness of windowing, so that a further exploration of domain redundancy is suggested as a promising area for further research.