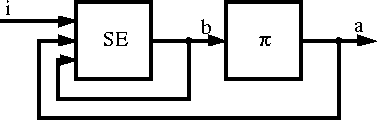
Figure 10: Structure of a POMDP agent.
Chrisman [22] showed how the forward-backward algorithm for learning HMMs could be adapted to learning POMDPs. He, and later McCallum [75], also gave heuristic state-splitting rules to attempt to learn the smallest possible model for a given environment. The resulting model can then be used to integrate information from the agent's observations in order to make decisions.
Figure 10 illustrates the basic structure for a perfect-memory controller. The component on the left is the state estimator, which computes the agent's belief state, b as a function of the old belief state, the last action a, and the current observation i. In this context, a belief state is a probability distribution over states of the environment, indicating the likelihood, given the agent's past experience, that the environment is actually in each of those states. The state estimator can be constructed straightforwardly using the estimated world model and Bayes' rule.

Figure 10: Structure of a POMDP agent.
Now we are left with the problem of finding a policy mapping belief states into action. This problem can be formulated as an MDP, but it is difficult to solve using the techniques described earlier, because the input space is continuous. Chrisman's approach [22] does not take into account future uncertainty, but yields a policy after a small amount of computation. A standard approach from the operations-research literature is to solve for the optimal policy (or a close approximation thereof) based on its representation as a piecewise-linear and convex function over the belief space. This method is computationally intractable, but may serve as inspiration for methods that make further approximations [20, 65].