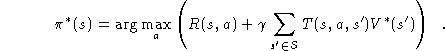Before we consider algorithms for learning to behave in MDP environments, we will explore techniques for determining the optimal policy given a correct model. These dynamic programming techniques will serve as the foundation and inspiration for the learning algorithms to follow. We restrict our attention mainly to finding optimal policies for the infinite-horizon discounted model, but most of these algorithms have analogs for the finite-horizon and average-case models as well. We rely on the result that, for the infinite-horizon discounted model, there exists an optimal deterministic stationary policy [10].
We will speak of the optimal value of a state--it is the
expected infinite discounted sum of reward that the agent will gain if
it starts in that state and executes the optimal policy. Using 
as a complete decision policy, it is written
This optimal value function is unique and can be defined as the solution to the simultaneous equations
which assert that the value of a state s is the expected instantaneous reward plus the expected discounted value of the next state, using the best available action. Given the optimal value function, we can specify the optimal policy as
