Markov Decision Processes

Problems with delayed reinforcement are well modeled as Markov decision processes (MDPs). An MDP consists of

• a set of states ,
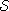• a set of actions ,
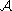• a reward function 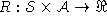, and
• a state transition function 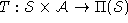, where a member of 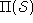is a probability distribution over the set 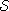(i.e. it maps states to probabilities). We write T(s,a,s') for the probability of making a transition from state s to state s' using action a.

The state transition function probabilistically specifies the next state of the environment as a function of its current state and the agent's action. The reward function specifies expected instantaneous reward as a function of the current state and action. The model is Markov if the state transitions are independent of any previous environment states or agent actions. There are many good references to MDP models [10, 13, 48, 90].

Although general MDPs may have infinite (even uncountable) state and action spaces, we will only discuss methods for solving finite-state and finite-action problems. In section 6, we discuss methods for solving problems with continuous input and output spaces.