The results of Section 5.1 suggest that the PU function is useful in identifying structure in data: clusterings optimized relative to this function were simpler and as accurate as clusterings that were not optimized relative to the function. Thus, PU leads to something reasonable along the error rate and simplicity dimensions, but can other objective functions do a better job along these dimensions? Based on earlier discussion on the limitations of PU, notably that averaging CU over the clusters of a partition introduced `cliffs' in the space of partitions, it is likely that better objective functions can be found. For example, we might consider Bayesian variants like those found in AUTOCLASS [Cheeseman et al., 1988] and Anderson and Matessa's [1991] system, or the closely related MML approach of SNOB [Wallace & Dowe, 1994]. We do not evaluate alternative measures such as these here, but do suggest a number of other candidates.
Section 2.1 noted that the CU function could be viewed as a summation over Gini Indices, which measured the collective impurity of variables conditioned on cluster membership. Intuition may be helped further by an information-theoretic analog to CU [Corter & Gluck, 1992]:
The information-theoretic analog
can be understood as a summation over information
gain values, where information gain is an often used selection
criterion for decision tree induction
[Quinlan, 1986]: the clustering analog rewards
clusters,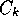 
, that maximize the sum of information gains over
the individual variables, 
.
Both the Gini and Information Gain measures are
often-used bases for selection measures of decision tree
induction. They are used to measure the expected decrease in
impurity or uncertainty of a class label, conditioned
on knowledge of a given variable's value. In a clustering
context, we are interested in the decrease in impurity
of each variable's value conditioned on knowledge
of cluster membership -- thus, we use a summation
over suitable Gini Indices or alternatively, information
gain scores. However, it is well known that in the context of decision
tree induction, both measures are biased to select variables with more
legal values. Thus, various normalizations of these measures
or different measures altogether, have been devised.
In the clustering adaptation of these measures normalization
is also necessary, since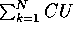 
alone or its information-theoretic
analog will favor a clustering of greatest cardinality, in which the
data are partitioned into
singleton clusters, one for each observation. Thus, PU normalizes
the sum of Gini indices by averaging.
A general observation is that many selection measures
used for decision tree induction can be
adapted as objective functions for clustering. There are a
number of selection measures that suggest themselves as
candidates for clustering, in which normalization is more principled
than averaging. Two candidates are Quinlan's [1986]
Gain Ratio and
Lopez de Mantaras' [1991] normalized information
gain.
[Quinlan, 1986]
[Lopez de Mantaras, 1991]
From these we can derive two objective functions for clustering:
The latter of these clustering variations was defined in Fisher and Hapanyengwi [1993]. Our nonsystematic experimentation with Lopez de Mantaras' normalized information gain variant suggests that it mitigates the problems associated with PU, though conclusions about its merits must await further experimentation. In general, there are a wealth of promising objective functions based on decision tree selection measures that we might consider. We have described two, but there are others such as Fayyad's [1991] ORT function.
The relationship between supervised and unsupervised measures also
has been pointed out in the context of Bayesian systems [Duda & Hart, 1973].
Consider AUTOCLASS [Cheeseman
et al.1988], which searches for
the most probable clustering, H, given the available data set,
D -- i.e.,
the clustering with highest 
. Under
independence assumptions made by AUTOCLASS, the computation
of 
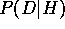includes the easily seen mechanisms of the simple Bayes
classifier used in supervised contexts.
We have not compared the proposed derivations of decision tree selection measures or the Bayesian/MML measures of AUTOCLASS and SNOB as yet, but have proposed pattern-completion error rate, simplicity, and classification cost as external, objective criteria that could be used in such comparisons. An advantage of the Bayesian and MML approaches is that, with proper selection of prior biases, these do not require a separate strategy (e.g., resampling) for pruning, and these strategies can be adapted for variable frontier identification. Rather, the objective function used for cluster formation serves to cease hierarchical decomposition as well. Though we know of no experimental studies with the Bayesian and MML techniques along the accuracy and cost dimensions outlined here, we expect that each would perform quite well.
JAIR, 4