The size of the MDP obtained, i.e. the number of e-states it contains is a
key issue for us, as it has to be amenable to state-based solution methods.
Ideally, we would like the MDP to be of minimal size. However, we do
not know of a method building the minimal equivalent MDP
incrementally, adding parts as required by the solution method.
And since in the worst case even the minimal equivalent MDP
can be larger than the NMRDP by a factor exponential in the length
of the reward formulae [2], constructing it
entirely would nullify the interest of anytime solution methods.
However, as we now explain, Definition 5 leads to
an equivalent MDP exhibiting a relaxed notion of minimality, and which
is amenable to incremental construction. By inspection, we may observe
that wherever an e-state
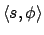 has a successor
has a successor
 via action
via action 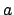 , this means that in order to
succeed in rewarding the behaviours described in
, this means that in order to
succeed in rewarding the behaviours described in 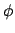 by means of
execution sequences that start by going from
by means of
execution sequences that start by going from 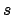 to
to 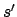 via
via 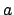 , it
is necessary that the future starting with
, it
is necessary that the future starting with 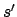 succeeds in rewarding
the behaviours described in
succeeds in rewarding
the behaviours described in  . If
. If
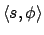 is in
the minimal equivalent MDP, and if there really are such execution
sequences succeeding in rewarding the behaviours described in
is in
the minimal equivalent MDP, and if there really are such execution
sequences succeeding in rewarding the behaviours described in 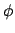 ,
then
,
then
 must also be in the minimal MDP. That
is, construction by progression can only introduce e-states which are
a priori needed. Note that an e-state that is a priori
needed may not really be needed: there may in fact be no
execution sequence using the available actions that exhibits a given
behaviour. For instance, consider the response formula
must also be in the minimal MDP. That
is, construction by progression can only introduce e-states which are
a priori needed. Note that an e-state that is a priori
needed may not really be needed: there may in fact be no
execution sequence using the available actions that exhibits a given
behaviour. For instance, consider the response formula
 , i.e., every time
trigger
, i.e., every time
trigger 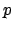 is true, we will be rewarded
is true, we will be rewarded 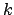 steps later provided
steps later provided 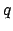 is true then. Obviously, whether
is true then. Obviously, whether 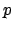 is true at some stage affects the
way future states should be rewarded. However, if the transition
relation happens to have the property that
is true at some stage affects the
way future states should be rewarded. However, if the transition
relation happens to have the property that 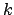 steps from a state
satisfying
steps from a state
satisfying 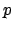 , no state satisfying
, no state satisfying 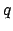 can be reached, then a
posteriori
can be reached, then a
posteriori 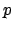 is irrelevant, and there was no need to label
e-states differently according to whether
is irrelevant, and there was no need to label
e-states differently according to whether 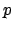 was true or not -
observe an occurrence of this in the example in Figure 7, and
how this leads FLTL to produce an extra state at
the bottom left of the Figure. To
detect such cases, we would have to look perhaps quite deep into
feasible futures, which we cannot do while constructing the e-states
on the fly. Hence the relaxed notion which we call blind
minimality does not always coincide with absolute minimality.
We now formalise the difference between true and blind minimality. For
this purpose, it is convenient to define some functions
was true or not -
observe an occurrence of this in the example in Figure 7, and
how this leads FLTL to produce an extra state at
the bottom left of the Figure. To
detect such cases, we would have to look perhaps quite deep into
feasible futures, which we cannot do while constructing the e-states
on the fly. Hence the relaxed notion which we call blind
minimality does not always coincide with absolute minimality.
We now formalise the difference between true and blind minimality. For
this purpose, it is convenient to define some functions  and
and
 mapping e-states
mapping e-states  to functions from
to functions from 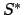 to
to  intuitively assigning rewards to sequences in the NMRDP starting from
intuitively assigning rewards to sequences in the NMRDP starting from
 . Recall from Definition 1 that
. Recall from Definition 1 that  maps each e-state of the MDP to the underlying NMRDP state.
maps each e-state of the MDP to the underlying NMRDP state.
Note carefully the difference between  and
and  . The former
describes the rewards assigned to all continuations of a given
state sequence, while the latter confines rewards to feasible
continuations. Note also that
. The former
describes the rewards assigned to all continuations of a given
state sequence, while the latter confines rewards to feasible
continuations. Note also that  and
and  are well-defined
despite the indeterminacy in the choice of
are well-defined
despite the indeterminacy in the choice of  , since by
clause 4 of Definition 1, all such choices lead to
the same values for
, since by
clause 4 of Definition 1, all such choices lead to
the same values for 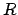 .
.
Theorem 3
Let 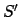 be the set of e-states in an equivalent MDP
be the set of e-states in an equivalent MDP 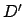 for
for
 .
. 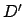 is minimal iff every e-state in
is minimal iff every e-state in
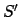 is reachable and
is reachable and 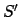 contains no two distinct e-states
contains no two distinct e-states 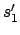 and
and 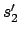 with
with
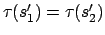 and
and
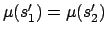 .
.
Proof: See Appendix B. 
Blind minimality is similar, except that, since there is no looking ahead, no
distinction can be drawn between feasible trajectories and others in the
future of 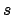 :
:
Definition 7
Let 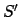 be the set of e-states in an equivalent MDP
be the set of e-states in an equivalent MDP 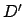 for
for
 .
. 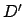 is blind minimal iff
every e-state in
is blind minimal iff
every e-state in 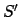 is reachable and
is reachable and 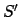 contains no two distinct
e-states
contains no two distinct
e-states 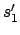 and
and 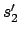 with
with
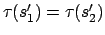 and
and
 .
.
Theorem 4
Let 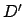 be the translation of
be the translation of 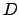 as in
Definition 5.
as in
Definition 5. 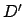 is a blind minimal
equivalent MDP for
is a blind minimal
equivalent MDP for 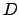 .
.
Proof:
See Appendix B. 
The size difference between the blind-minimal and minimal MDPs will
depend on the precise interaction between rewards and dynamics for the
problem at hand, making theoretical analyses difficult and
experimental results rather anecdotal. However, our experiments in
Section 5 and 6 will show that
from a computation time point of view, it is often preferable to work
with the blind-minimal MDP than to invest in the overhead of computing
the truly minimal one.
Finally, recall that syntactically different but semantically
equivalent reward function specifications define the same
e-state. Therefore, neither minimality nor blind minimality can be
achieved in general without an equivalence check at least as complex
as theorem proving for LTL. In pratical implementations, we avoid
theorem proving in favour of embedding (fast) formula simplification
in our progression and regression algorithms. This means that in
principle we only approximate minimality and blind minimality, but
this appears to be enough for practical purposes.
Sylvie Thiebaux
2006-01-20

