Translation Into MDP
We now exploit the compact representation of a non-Markovian reward
function as a reward function specification to translate an NMRDP into
an equivalent MDP amenable to state-based anytime solution methods.
Recall from Section 2 that each e-state in the MDP
is labelled by a state of the NMRDP and by history information
sufficient to determine the immediate reward. In the case of a compact
representation as a reward function specification 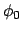 , this
additional information can be summarised by the progression of
, this
additional information can be summarised by the progression of
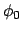 through the sequence of states passed through. So an e-state
will be of the form
through the sequence of states passed through. So an e-state
will be of the form
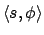 , where
, where 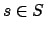 is a
state, and
is a
state, and
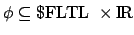 is a reward function
specification (obtained by progression). Two e-states
is a reward function
specification (obtained by progression). Two e-states
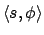 and
and
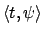 are equal if
are equal if  , the
immediate rewards are the same, and the results of progressing
, the
immediate rewards are the same, and the results of progressing 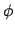 and
and 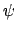 through
through 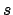 are semantically equivalent.8
are semantically equivalent.8
Definition 5
Let
 be an NMRDP, and
be an NMRDP, and 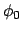 be a
reward function specification representing
be a
reward function specification representing 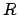 (i.e.,
(i.e.,
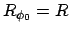 , see
Definition 4).
We translate
, see
Definition 4).
We translate 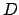 into the MDP
into the MDP
 defined as follows:
defined as follows:
-

-

-

- If
 , then
, then


If
 , then
, then
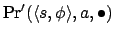 is undefined
is undefined
-

- For all
 ,
, 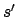 is reachable under
is reachable under  from
from 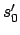 .
.
Item 1 says that the e-states are labelled by a state and a reward
function specification. Item 2 says that the initial e-state is
labelled with the initial state and with the original reward function
specification. Item 3 says that an action is applicable in an e-state
if it is applicable in the state labelling it. Item 4 explains how
successor e-states and their probabilities are computed. Given an
action 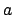 applicable in an e-state
applicable in an e-state
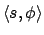 , each
successor e-state will be labelled by a successor state
, each
successor e-state will be labelled by a successor state 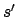 of
of 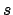 via
via
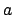 in the NMRDP and by the progression of
in the NMRDP and by the progression of 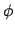 through
through 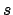 . The
probability of that e-state is
. The
probability of that e-state is 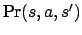 as in the NMRDP. Note
that the cost of computing
as in the NMRDP. Note
that the cost of computing 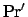 is linear in that of computing
is linear in that of computing  and in the sum of the lengths of the formulae in
and in the sum of the lengths of the formulae in 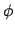 . Item 5 has
been motivated before (see Section 3.6). Finally, since
items 1-5 leave open the choice of many MDPs differing only in the
unreachable states they contain, item 6 excludes all such irrelevant
extensions.
It is easy to show that this translation leads to an equivalent MDP,
as defined in Definition 1. Obviously, the function
. Item 5 has
been motivated before (see Section 3.6). Finally, since
items 1-5 leave open the choice of many MDPs differing only in the
unreachable states they contain, item 6 excludes all such irrelevant
extensions.
It is easy to show that this translation leads to an equivalent MDP,
as defined in Definition 1. Obviously, the function
 required for Definition1 is given by
required for Definition1 is given by
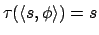 , and then
the proof is a matter of checking conditions.
In our practical implementation, the labelling is one step ahead of
that in the definition: we label the initial e-state with
, and then
the proof is a matter of checking conditions.
In our practical implementation, the labelling is one step ahead of
that in the definition: we label the initial e-state with
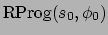 and compute the current reward and the current
reward specification label by progression of predecessor reward
specifications through the current state rather than through the
predecessor states. As will be apparent below, this has the potential
to reduce the number of states in the generated MDP.
Figure 7 shows the equivalent MDP produced for the
$FLTL version of our NMRDP example in Figure 3.
Recall that for this example, the PLTL reward formula was
and compute the current reward and the current
reward specification label by progression of predecessor reward
specifications through the current state rather than through the
predecessor states. As will be apparent below, this has the potential
to reduce the number of states in the generated MDP.
Figure 7 shows the equivalent MDP produced for the
$FLTL version of our NMRDP example in Figure 3.
Recall that for this example, the PLTL reward formula was
 . In
$FLTL, the allocation of rewards is described by
. In
$FLTL, the allocation of rewards is described by
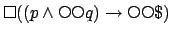 . The figure also shows the
relevant formulae labelling the e-states, obtained by
progression of this reward formula. Note that without progressing one step
ahead, there would be 3 e-states with state
. The figure also shows the
relevant formulae labelling the e-states, obtained by
progression of this reward formula. Note that without progressing one step
ahead, there would be 3 e-states with state  on the
left-hand side, labelled with
on the
left-hand side, labelled with  ,
, 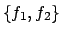 , and
, and
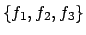 ,
respectively.
,
respectively.
Figure 7:
Equivalent MDP Produced by FLTL
|
![$\textstyle \parbox{0.55\textwidth}{\includegraphics[height=0.4\textheight]{figures/pqfltl}}$](img333.png)  |
Sylvie Thiebaux
2006-01-20

