

Next: Exploiting symmetry by changing
Up: Symmetry
Previous: Symmetry
One way
to exploit symmetry is to modify the set of axioms in a way that
captures the power of the symmetry. In the pigeonhole problem, for example, we can
argue that since there is a symmetry under the exchange of pigeons or
of holes, we can assume ``without loss of generality'' that pigeon 1
is in hole 1, and then by virtue of a residual symmetry that pigeon 2
is in hole 2, and so on.
The basic idea is to add so-called symmetry-breaking axioms to
our original theory, axioms that break the existing symmetry without
affecting the overall satisfiability of the theory itself. This idea
was introduced by Crawford et al. Ginsberg:symmetry.
While attractive in theory, there are at least two fundamental
difficulties with the symmetry-breaking approach:
- Luks and Roy Luks:symmetry have shown that breaking
all of the symmetries in any particular problem may require the
introduction of a set of symmetry-breaking axioms of exponential size.
This problem can be sidestepped by breaking only ``most'' of the
symmetries, although little is known about how the set of broken
symmetries is to be selected.
- Far more serious, the technique can only be applied if the
symmetry in question is global. This is because the basic argument
that satisfiability is unaffected by the introduction of the new
axioms requires that there be no additional axioms to consider.
In theoretical problems, global symmetries exist. But in practice,
even the addition of asymmetric axioms that constrain the problem
further (e.g., you can't put pigeon 4 in hole 7) will break the
required global symmetry and render this method inapplicable. More
problematic still is the possibility of the symmetries being
``obscured'' by replacing the single axiom
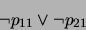 |
(41) |
with the equivalent pair
and
from which (41) can obviously be recovered using resolution.
Once again, the symmetry in the original problem has vanished and the
method cannot be applied.
These arguments could perhaps have been anticipated by consideration
of our usual table; since the inference mechanism itself is not
modified (and it is possible to break global symmetries), none of the
entries has changed. Let us turn, then, to other techniques that
modify inference itself.


Next: Exploiting symmetry by changing
Up: Symmetry
Previous: Symmetry
Matt Ginsberg
2004-02-19