 |
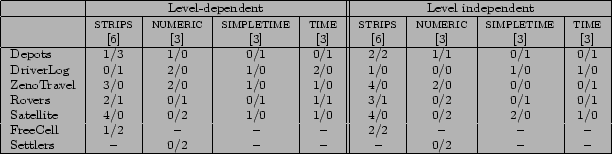
The tables are organised as follows: the rows correspond to domains, as labelled, and the columns to the levels considered and the number of planners used. The number of planners varies between columns because different planners participated at the different domain levels. For example, more planners participated at the STRIPS level than at any of the others. When planners produced too little data to justify statistical analysis they were not included in the tests. Thus, of the eleven fully-automated planners in the competition seven produced enough data for analysis in these experiments.
The cells of the tables contain two integer values separated by a diagonal. The value on the left of the diagonal indicates the number of planners that found the problems in the corresponding domain and level significantly easy. The value on the right indicates the number that found those problems significantly hard. Thus, it can be seen in Figure 22 that of the six fully-automated planners that participated at the STRIPS level of the Depots domain, one found the problems easy and three found them hard. For the other two planners the areas calculated using the method explained above were not found to be sufficiently extreme for rejection of the null hypothesis. Broadly speaking (we discuss the interpretation of the data in detail below) the four left-hand columns tell us whether the problems in a particular domain and level were easy or hard relative to other problems at that level; the four right-hand columns tell us whether they were easy or hard relative to all other problems. In addition, the rows allow us to compare domains for relative difficulty: for example, none of the planners found ZenoTravel to be hard at any level relative to other problems at the same level, whilst Depots and Rovers were found to be hard by at least one competitor at all levels.
The level-independent tests are reported in exactly the same way in the right-hand halves of Figures 22 (for the fully-automated comparison) and 23 (for the hand-coded comparison). These tables tell us whether the problems in a particular domain and level are easy or hard relative to problems from other domains irrespective of level.
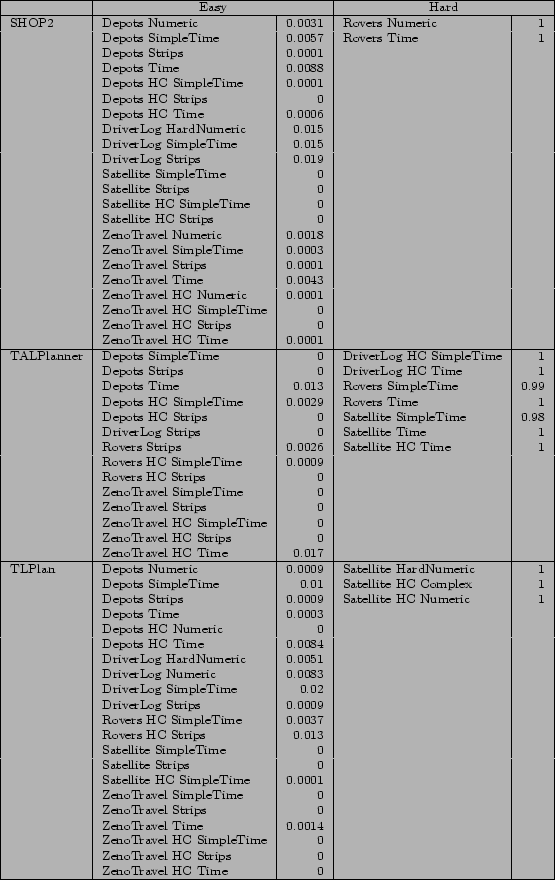
The data presented in Figures 24 and 25 show which planners found which domain-level combinations easy or hard as discussed with reference to the tables in Figures 22 and 23. This information might contribute to an understanding about which planning approaches are likely to be suited to what kinds of problems, although further analysis would be needed to pursue this question.
The tables are organised as follows. There is a row for each of the individual planners, indicating which domain-level combinations were found to be easy or hard for the corresponding planner. Associated with the categorization of a combination as easy or hard is the p-value indicating the statistical significance of this finding. We have presented only the findings that were significant at the 5% level. Because this is a two-tailed test (we had no a priori knowledge to help us to determine whether a problem would be easy or hard) the critical value at the easy end is 0.025. At the hard end the critical value is 0.975. Figure 24 shows our findings for the fully-automated planners. Figure 25 shows the same information with respect to the hand-coded planners.
 |