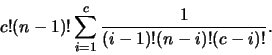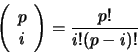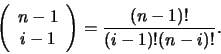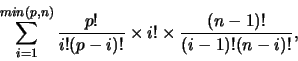Next: Our Solution: WOLFIE
Up: The WOLFIE Algorithm and
Previous: The WOLFIE Algorithm and
Solving the Lexicon Acquisition Problem
A first attempt to solve the Lexicon Acquisition Problem might be to
examine all interpretation functions across the corpus, then choose
the one(s) with minimal lexicon size. The number of possible interpretation
functions for a given input pair is dependent on both the size of the
sentence and its representation. In a sentence with w words, there
are
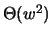 possible phrases, not a particular challenge.
However, the number of possible interpretation functions grows
extremely quickly with the size of the input. For a sentence with p
phrases and an associated tree with n vertices, the number of possible
interpretation functions is:
possible phrases, not a particular challenge.
However, the number of possible interpretation functions grows
extremely quickly with the size of the input. For a sentence with p
phrases and an associated tree with n vertices, the number of possible
interpretation functions is:
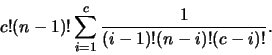 |
(1) |
where c is min(p,n). The derivation of the above formula is as follows.
We must choose which phrases to use in the domain of f, and we
can choose one phrase, or two, or any number up to
min(p,n) (if n<p we can only assign n phrases since
f is one-to-one),
or
where i is the number of phrases chosen.
But we can also permute these phrases, so that
the ``order'' in which they are assigned to the vertices is different.
There are i! such permutations.
We must also choose which vertices to
include in the range of the interpretation function.
We have to choose the root each time,
so if we are choosing i vertices, we have n-1 choose i-1
vertices left after choosing the root, or
The full number
of possible interpretation functions is then:
which simplifies to Equation 1.
When n=p, the largest term of this equation
is c!=p!, which grows at least exponentially
with p, so in general the number of interpretation functions is too
large to allow enumeration. Therefore, finding a lexicon by examining
all interpretations across the corpus, then choosing the lexicon(s) of
minimum size, is clearly not tractable.
Instead of finding all interpretations, one could find a set of
candidate meanings for each phrase, from which the final meaning(s)
for that phrase could be chosen in a way that minimizes lexicon size.
One way to find candidate meanings is to fracture
the meanings of sentences in which a phrase
appears. Siskind (1993) defined fracturing (he also calls it
the UNLINK* operation) over terms such that the result includes all
subterms of an expression plus  .
In our representation formalism, this corresponds to finding all possible
connected subgraphs of a meaning, and adding the empty graph.
Like the interpretation function technique just discussed,
fracturing would also lead to an
exponential blowup in the number of candidate meanings for a phrase: A
lower bound on the number of connected subgraphs for a full binary
tree with n vertices is obtained by noting that any subset of the
(n+1)/2 leaves may be deleted and still maintain connectivity of the
remaining tree. Thus, counting all of the ways that leaves can be
deleted gives us a lower bound of
2(n+1)/2
fractures.6
This does not completely rule out fracturing as part
of a technique for lexicon learning since trees do not tend to get
very large, and indeed Siskind uses it in
many of his systems, with other constraints to help control the
search. However, we wish to avoid any chance of exponential blowup to
preserve the generality of our approach for other tasks.
Another option is to force CHILL to essentially induce a lexicon on
its own. In this model, we would provide to CHILL an ambiguous
lexicon in which each phrase is paired with every fracture of every
sentence in which it appears. CHILL would then have to decide which
set of fractures leads to the correct parse for each training
sentence, and would only include those in a final learned
parser-lexicon combination. Thus the search would again become exponential.
Furthermore, even with small representations, it would likely lead to a system
with poor generalization ability. While some of Siskind's
work (e.g., Siskind, 1992) took syntactic constraints into account
and did not encounter such difficulties, those versions did not handle
lexical ambiguity.
If we could efficiently find some good candidates, a standard
induction algorithm could then attempt to use them as a source of
training examples for each phrase. However, any attempt to use the
list of candidate meanings of one phrase as negative examples for another
phrase would be flawed.
The learner could not know in advance which phrases are possibly
synonymous, and thus which phrase lists to use as negative examples of
other phrase meanings. Also, many representation components would be
present in the lists of more than one phrase. This is a source of
conflicting evidence for a learner, even without the presence of
synonymy. Since only positive examples are available, one might think
of using most specific conjunctive learning, or finding the
intersection of all the representations for each phrase, as proposed
by Anderson (1977). However,
the meanings of an ambiguous phrase are disjunctive, and
this intersection would be empty. A similar difficulty would be
expected with the positive-only compression of Muggleton (1995).
.
In our representation formalism, this corresponds to finding all possible
connected subgraphs of a meaning, and adding the empty graph.
Like the interpretation function technique just discussed,
fracturing would also lead to an
exponential blowup in the number of candidate meanings for a phrase: A
lower bound on the number of connected subgraphs for a full binary
tree with n vertices is obtained by noting that any subset of the
(n+1)/2 leaves may be deleted and still maintain connectivity of the
remaining tree. Thus, counting all of the ways that leaves can be
deleted gives us a lower bound of
2(n+1)/2
fractures.6
This does not completely rule out fracturing as part
of a technique for lexicon learning since trees do not tend to get
very large, and indeed Siskind uses it in
many of his systems, with other constraints to help control the
search. However, we wish to avoid any chance of exponential blowup to
preserve the generality of our approach for other tasks.
Another option is to force CHILL to essentially induce a lexicon on
its own. In this model, we would provide to CHILL an ambiguous
lexicon in which each phrase is paired with every fracture of every
sentence in which it appears. CHILL would then have to decide which
set of fractures leads to the correct parse for each training
sentence, and would only include those in a final learned
parser-lexicon combination. Thus the search would again become exponential.
Furthermore, even with small representations, it would likely lead to a system
with poor generalization ability. While some of Siskind's
work (e.g., Siskind, 1992) took syntactic constraints into account
and did not encounter such difficulties, those versions did not handle
lexical ambiguity.
If we could efficiently find some good candidates, a standard
induction algorithm could then attempt to use them as a source of
training examples for each phrase. However, any attempt to use the
list of candidate meanings of one phrase as negative examples for another
phrase would be flawed.
The learner could not know in advance which phrases are possibly
synonymous, and thus which phrase lists to use as negative examples of
other phrase meanings. Also, many representation components would be
present in the lists of more than one phrase. This is a source of
conflicting evidence for a learner, even without the presence of
synonymy. Since only positive examples are available, one might think
of using most specific conjunctive learning, or finding the
intersection of all the representations for each phrase, as proposed
by Anderson (1977). However,
the meanings of an ambiguous phrase are disjunctive, and
this intersection would be empty. A similar difficulty would be
expected with the positive-only compression of Muggleton (1995).



Next: Our Solution: WOLFIE
Up: The WOLFIE Algorithm and
Previous: The WOLFIE Algorithm and
Cindi Thompson
2003-01-02