

Next: Application of SMOTE to
Up: Future Work
Previous: SMOTE-NC
Potentially,
SMOTE can also be extended for nominal features -- SMOTE-N -- with the nearest neighbors computed using the modified version of Value Difference Metric [36]
proposed by Cost and Salzberg (1993). The Value Difference Metric (VDM) looks at the overlap of feature values over all feature vectors. A matrix defining the distance between corresponding feature values
for all feature vectors is created. The distance 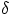 between two corresponding feature values
is defined as follows.
between two corresponding feature values
is defined as follows.
|  |
(1) |
In the above equation, V1 and V2 are the two corresponding feature values. C1 is the total
number of occurrences of feature value V1, and C1i is the number of occurrences of feature
value V1 for class i. A similar convention can also be applied to C2i and C2.
k is a constant, usually set to 1. This equation is used to compute the matrix of value differences
for each nominal feature in the given set of feature vectors. Equation 1 gives a geometric
distance on
a fixed, finite set of values [37]. Cost and Salzberg's modified VDM omits the weight term wfa
included
in the 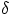 computation by Stanfill and Waltz, which has an effect of making
computation by Stanfill and Waltz, which has an effect of making 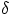 symmetric.
The distance
symmetric.
The distance  between two feature vectors is given by:
between two feature vectors is given by:
|  |
(2) |
r = 1 yields the Manhattan distance, and r = 2 yields the Euclidean distance [37]. wx and wy are the exemplar weights in the modified VDM. wy = 1 for a new example (feature vector),
and wx is the bias towards more reliable examples (feature vectors) and is computed as the ratio of the
number of uses of a feature vector to the number of correct uses of the feature vector; thus, more accurate
feature vectors will have wx 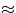 1. For SMOTE-N we can ignore these weights in equation 2, as SMOTE-N is not used for classification purposes directly. However, we can redefine these
weights to give more weight to the minority class feature vectors falling closer to the majority class
feature vectors; thus, making those minority class features appear further away from the feature vector under
consideration. Since,
we are more interested in forming broader but accurate regions of the minority class, the weights
might be used to
avoid populating along neighbors which fall closer to the majority class.
To generate new minority class feature vectors, we can create new set feature values by taking the
majority vote of the feature vector in consideration and its k nearest neighbors. Table 6.2
shows an example of creating a synthetic feature vector.
1. For SMOTE-N we can ignore these weights in equation 2, as SMOTE-N is not used for classification purposes directly. However, we can redefine these
weights to give more weight to the minority class feature vectors falling closer to the majority class
feature vectors; thus, making those minority class features appear further away from the feature vector under
consideration. Since,
we are more interested in forming broader but accurate regions of the minority class, the weights
might be used to
avoid populating along neighbors which fall closer to the majority class.
To generate new minority class feature vectors, we can create new set feature values by taking the
majority vote of the feature vector in consideration and its k nearest neighbors. Table 6.2
shows an example of creating a synthetic feature vector.
Table 7:
Example of SMOTE-N
| Let F1 = A B C D E be the feature vector under consideration |
| and let its 2 nearest neighbors be |
| F2 = A F C G N |
| F3 = H B C D N |
| The application of SMOTE-N would create the following feature vector: |
| FS = A B C D N |
| |


Next: Application of SMOTE to
Up: Future Work
Previous: SMOTE-NC
Nitesh Chawla (CS)
6/2/2002


![]() computation by Stanfill and Waltz, which has an effect of making
computation by Stanfill and Waltz, which has an effect of making ![]() symmetric.
The distance
symmetric.
The distance ![]() between two feature vectors is given by:
between two feature vectors is given by:
