Stable Model Semantics

Stable model semantics ( SM) was introduced by Gelfond and Lifschitz [18] as a tool to provide a semantics for logic programs with negation. their original proposal is now one of the standard semantics for logic programs. We now recall the definition of propositional stable model.

Let $P$ be a propositional, general logic program. Let $M$ be a subset (i.e., an interpretation) of the atoms of $P$. Let $P^{M}$ be the program obtained from $P$ in the following way: if a clause $C$ of $P$ contains in its body a negated atom $\neg A$ such that $A \in M$ then $C$ is deleted; if a body of a clause contains a negated atom $\neg A$ such that $A \not\in M$ then $\neg A$ is deleted from the body of the clause. If $M$ is a least Herbrand model of $P^{M}$ then $M$ is a stable model of $P$.

For the formalism SM, we consider the program $P$ as the knowledge base. We write $P \models_{\textsc{sm}} Q$ to denote that query $Q$ is implied by a logic program $P$ under Stable Model semantics.

In order to prove our result, we need to define the kernel of a graph.

Definition 12 (Kernel)   Let $G=(V,E)$ be a graph. A kernel of $G$ is a set $K \subseteq V$ such that, denoting $H=V-K$, it holds:

1. $H$ is a vertex cover of $G$
2. for all $j \in H$, there exists an $i \in K$ such that $(i,j) \in E$.

We can now state the theorem on the compilability class of inference in the stable model semantics, and the corresponding theorem compactness class.

Theorem 8   The problem of inference for the Stable Model semantics is $\parallel\!\leadsto$ coNP-complete, thus Stable Model Semantics is thm-coNPcomplete.

Proof. Membership in the class follows from the fact that the problem is coNP-complete [40]. For the hardness, we adapt the proof of Marek and Truszczynski [40] showing that deciding whether a query is true in all stable models is coNP-hard.

Let $\epsilon$KERNEL be the language $\{ \epsilon, G\}$ such that $G$ is a graph with at least one kernel. Let $\vert G\vert=n$, and observe that $G$ cannot have more vertices than its size $n$.

We show that for each $n$, there exists a logic program $P_{n}$ such that for every graph $G$ with at most $n$ vertices, there exists a query $Q_{G}$ such that $G$ has a kernel iff $P_{n} \not\models_{\textsc{sm}} Q_{G}$.

Let the alphabet of $P_{n}$ be composed by the following $2n^{2}+n$ propositional letters: $\{ a_{i} \vert i \in\{1..n\} ~ \} \cup \{ r_{ij}, s_{ij} \vert i,j \in \{1..n\} ~\}$.

The program $P_{n}$ is defined as:

$$\left. \begin{array}{rcl} a_{j} & ~:\!\!-~& \neg a_{i}, r_{i... ...-~& \neg s_{ij} \end{array}\right\} \mbox{for } i,j\in\{1..n\}$$

Given a graph $G=(V,E)$, the query $Q_{G}$ is defined as

$$Q_{G} = (\bigvee_{(i,j)\in E} \neg r_{ij}) \vee (\bigvee_{(i,j)\not\in E} r_{ij})$$

The reduction from $\epsilon$KERNEL to SM is defined as: $f_{1}(x,n) = P_{n}$, i.e., $f_{1}$ depends only on its second argument, $f_{2}(x, n) = \epsilon$, i.e., $f_{2}$ is a constant function, and $g = Q_{y}$, i.e., given a graph $G$, the circuit $g$ computes the query $Q_{G}$.

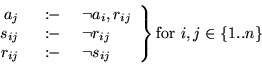
As a result, this is a $\parallel\!\leadsto$ reduction. We now show that this reduction is correct, i.e., $\langle \epsilon, G \rangle \in \epsilon$KERNEL ($G$ has a kernel) iff $P_{n} \not\models_{SM} Q_{G}$.

If-part. Suppose $P_{n} \not\models_{SM} Q_{G}$. Then, there exists a stable model $M$ of $P_{n}$ such that $M \models \neg Q_{G}$. Observe that $\neg Q_{G}$ is equivalent to the conjunction of all $r_{ij}$ such that $(i,j) \in E$, and all $\neg r_{ij}$ such that $(i,j)\not\in E$. Simplifying $P_{n}$ with $\neg Q_{G}$ we obtain the clauses:

$$a_{j} ~:\!\!-~\neg a_{i}, \mbox{ for } (i,j) \in E$$ (1)

Observe that $M$ contains all $s_{ij}$ such that $(i,j)\not\in E$, and in order to be stable, -- i.e., to support atoms $r_{ij}$ such that $(i,j) \in E$ -- $M$ contains no atom $s_{ij}$ such that $(i,j) \in E$.

Let $H= \{ j \vert a_{j} \in M \}$, $K = \{ i \vert a_{i} \not\in M \}$. Now $H$ is a vertex cover of G, since for each edge $(i,j) \in E$, $M$ should satisfy the corresponding clause (1) $a_{j} ~:\!\!-~\neg a_{i}$, hence either $a_{i} \in M$, or $a_{j} \in M$. Moreover, for each $j$ in $H$, the atom $a_{j}$ is in $M$, and since $M$ is a stable model, there exists a clause $a_{j} ~:\!\!-~\neg a_{i}$ such that $a_{i} \not\in M$, that is, $i \in K$. Therefore, $K$ is a kernel of $G$.

Only-if part. Suppose $G=(V,E)$ has a kernel $K$, and let $H=V-K$. Let $M$ be the interpretation

$$M = \{ r_{ij} \vert (i,j) \in E \} \cup \{ s_{ij} \vert (i,j) \not\in E \} \cup \{ a_{j} \vert j \in H \}$$

Obviously, $M \not\models Q_{G}$. We now show that $M$ is a stable model of $P_{n}$, i.e., $M$ is a least Herbrand model of $P_{n}^{M}$. In fact, $P_{n}^{M}$ contains the following clauses:

$$s_{ij} \mbox{ for } (i,j) \not\in E$$ (2)

$$r_{ij} \mbox{ for } (i,j) \in E$$ (3)

$$a_{j} ~:\!\!-~r_{ij} \mbox{ for } i \in K$$ (4)

Clauses in the last line are obtained from clauses in $P_{n}$ of the form $a_{j} ~:\!\!-~\neg a_{i}, r_{ij}$, where the clauses such that $i \in H$ (hence $a_{i} \in M$) are deleted, while in the other clauses the negated atom $\neg a_{i}$ is deleted, since $i \in K$, hence $a_{i} \not\in M$. Now for each $a_{j} \in M$, the vertex $j$ is in $H$, hence there is an edge $(i,j) \in E$, and $i \in K$. Hence clauses (4) and (3) are in $P_{n}^{M}$, hence in the least Herbrand model of $P_{n}^{M}$ there are exactly all $a_{j}$ such that $j \in H$.