Implementations of Markov Localization

The reader may notice that the principle of Markov localization leaves open

1. how the robot's belief Bel(L) is represented and
2. how the conditional probabilities 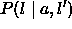and are computed.

Accordingly, existing approaches to Markov localization mainly differ in the representation of the state space and the computation of the perceptual model. In this section we will briefly discuss different implementations of Markov localization focusing on these two topics (see Section 5 for a more detailed discussion of related work).

1. State Space Representations: A very common approach for the representation of the robots belief Bel(L) is based on Kalman filtering [Kalman1960, Smith et al. 1990] which rests on the restrictive assumption that the position of the robot can be modeled by a unimodal Gaussian distribution. Existing implementations [Leonard & Durrant-Whyte1992, Schiele & Crowley1994, Gutmann & Schlegel1996, Arras & Vestli1998] have proven to be robust and accurate for keeping track of the robot's position. Because of the restrictive assumption of a Gaussian distribution these techniques lack the ability to represent situations in which the position of the robot maintains multiple, distinct beliefs (c.f. 2). As a result, localization approaches using Kalman filters typically require that the starting position of the robot is known and are not able to re-localize the robot in the case of localization failures. Additionally, Kalman filters rely on sensor models that generate estimates with Gaussian uncertainty. This assumption, unfortunately, is not met in all situations (see for example [Dellaert et al. 1999]).

   To overcome these limitations, different approaches have used increasingly richer schemes to represent uncertainty in the robot's position, moving beyond the Gaussian density assumption inherent in the vanilla Kalman filter. [Nourbakhsh et al. 1995, Simmons & Koenig1995, Kaelbling et al. 1996] use Markov localization for landmark-based corridor navigation and the state space is organized according to the coarse, topological structure of the environment and with generally only four possible orientations of the robot. These approaches can, in principle, solve the problem of global localization. However, due to the coarse resolution of the state representation, the accuracy of the position estimates is limited. Topological approaches typically give only a rough sense as to where the robot is. Furthermore, these techniques require that the environment satisfies an orthogonality assumption and that there are certain landmarks or abstract features that can be extracted from the sensor data. These assumptions make it difficult to apply the topological approaches in unstructured environments.

2. Sensor Models: In addition to the different representations of the state space various perception models have been developed for different types of sensors (see for example [Moravec1988, Kortenkamp & Weymouth1994, Simmons & Koenig1995, Burgard et al. 1996, Dellaert et al. 1999, Konolige1999]). These sensor models differ in the way how they compute the probability of the current measurement. Whereas topological approaches such as [Kortenkamp & Weymouth1994, Simmons & Koenig1995, Kaelbling et al. 1996] first extract landmark information out of a sensor scan, the approaches in [Moravec1988, Burgard et al. 1996, Dellaert et al. 1999, Konolige1999] operate on the raw sensor measurements. The techniques for proximity sensors described in [Moravec1988, Burgard et al. 1996, Konolige1999] mainly differ in their efficiency and how they model the characteristics of the sensors and the map of the environment.

In order to combine the strengths of the previous representations, our approach relies on a fine and less restrictive representation of the state space ([Burgard et al. 1996, Burgard et al. 1998b, Fox1998]). Here the robot's belief is approximated by a fine-grained, regularly spaced grid, where the spatial resolution is usually between 10 and 40 cm and the angular resolution is usually 2 or 5 degrees. The advantage of this approach compared to the Kalman-filter based techniques is its ability to represent multi-modal distributions, a prerequisite for global localization from scratch. In contrast to the topological approaches to Markov localization, our approach allows accurate position estimates in a much broader range of environments, including environments that might not even possess identifiable landmarks. Since it does not depend on abstract features, it can incorporate raw sensor data into the robot's belief. And it typically yields results that are an order of magnitude more accurate. An obvious shortcoming of the grid-based representation, however, is the size of the state space that has to be maintained. Section 3.4 addresses this issue directly by introducing techniques that make it possible to update extremely large grids in real-time.