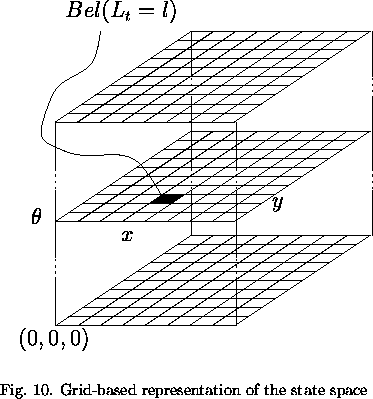
We will now return to the issue of how to represent and compute the belief distribution of the robot efficiently, describing what one might think of as the ``nut and bolts'' of grid-based Markov localization. Recall that to obtain accurate metric position estimates, our approach to Markov localization uses a fine-grained discretization of the state space. Here L is represented by a three-dimensional, regularly spaced grid, where the spatial resolution is usually between 10cm and 40cm and the angular resolution is usually 2 or 5 degrees. Figure 10 illustrates the structure of a position probability grid. Each layer of such a grid corresponds to all possible poses of the robot with the same orientation.
While such a fine-grained approximation makes it possible to estimate
the robot's position with high accuracy, an obvious disadvantage of
such a fine-grained discretization lies in the huge state space which
has to be maintained. For a mid-size environment of size
m 
, an angular grid resolution of 
, and a cell
size of 
cm the state space consists of 7,200,000
states. The basic Markov localization algorithm updates each of these
states for each sensory input and each atomic movement of the robot.
Current computer speed, thus, makes it impossible to update matrices
of this size in real-time.
To update such state spaces efficiently, we have developed two
techniques, which are described in the remainder of this section. The
first method, introduced in Section 3.4.1,
pre-computes the sensor model. It allows us to determine the likelihood
of sensor measurements by two look-up
operations--instead of expensive ray tracing operations. The second
optimization, described in Section 3.4.2,
is a selective update strategy. This strategy focuses the
computation, by only updating the relevant part of the state
space. Based on these two techniques, grid-based Markov localization
can be applied on-line to estimate the position of a mobile robot
during its operation, using a low-cost PC.
