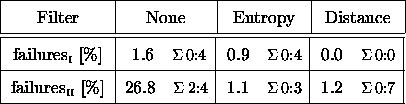
Table 2: Ability to track the robot's position.
In our first series of experiments, we were interested in comparing the ability of all three approaches--plain Markov localization without filtering, localization with the entropy filter, and localization with the distance filter--to keep track of the robot's position under normal working conditions. All three approaches tracked the robot's position in the empty museum well (first dataset), exhibiting only negligible errors in localization. The results obtained for the second, more challenging dataset, however, were quite different. In a nutshell, both filter-based approaches tracked the robot's position accurately, whereas conventional Markov localization failed frequently. Thus, had we used the latter in the museum exhibit, it would inevitably have led to a large number of collisions and other failures.

Table 2: Ability to track the robot's position.
Table 2 summarizes the results obtained for the different approaches in this tracking experiment. The first row of Table 2 provides the percentage of failures for the different filters on the first dataset (error values represent 95% confidence intervals). Position estimates were considered a ``failure'' if the estimated location of the robot deviated from the reference path by more than 45cm for at least 20 seconds. The percentage is measured in time during which the position was lost, relative to the total time of the dataset.
As can be seen here, all three approaches work well, and the distance filter provides the best performance. The second row provides the failures on the second dataset. While plain Markov localization failed in 26.8% of the overall time, both filter techniques show almost equal results with a failure of less than 2%. Thus, the two filter techniques are robust in highly dynamic environments, plain Markov localization is prone to fail.
To shed light onto the question as to why Markov localization performs so poorly when compared to the filter algorithms, we analyzed the sensor readings that each method used during the localization task. Figure 14 shows, for a a small fraction of the data, the measurements incorporated into the robot's belief by the three different approaches. Shown there are the end points of the sensor measurements used for localization relative to the positions on the reference path. Obviously, both filter approaches manage to focus their attention on the ``correct'' sensor measurements, whereas plain Markov localization incorporates massive amounts of corrupted (misleading) measurements. As also illustrated by Figure 14, both filter-based approaches produce more accurate results with a higher certainty in the correct position.