The upper and lower bounds for individual conditional probability distributions that form the basis of our variational method are based on the ``dual'' or ``conjugate'' representations of convex functions. We present a brief description of convex duality in this appendix, and refer the reader to Rockafellar (1970) for a more extensive treatment.
Let f(x) be a real-valued, convex function defined on a convex
set X (for example, 
). For simplicity of exposition, we
assume that f is a well-behaved (differentiable) function. Consider
the graph of f, i.e., the points (x,f(x)) in an n+1 dimensional
space. The fact that the function f is convex translates into
convexity of the set 
called the
epigraph of f and denoted by epi(f) (Figure 13).
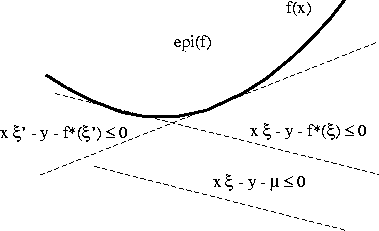
Figure 13: Half-spaces containing the convex set epi(f). The conjugate function
defines the critical half-spaces whose intersection is
epi(f), or, equivalently, it defines the tangent planes of f(x).
It is an elementary property of convex sets that they can be represented as the intersection of all the half-spaces that contain them (see Figure 13). Through parameterizing these half-spaces we obtain the dual representations of convex functions. To this end, we define a half-space by the condition:
where 
and 
parameterize all (non-vertical) half-spaces. We
are interested in characterizing the half-spaces that contain the
epigraph of f. We require therefore that the points in the epigraph
must satisfy the half-space condition: for 
, we must
have 
. This holds whenever 
as the points in the epigraph have the property that
. Since the condition must be satisfied by all 
,
it follows that
as well. Equivalently,
where the right-hand side of this equation defines a function
of , which is known as the ``dual'' or ``conjugate'' function
. This function, which is also a convex function, defines the
critical half-spaces which are needed for the representation of
epi(f) as an intersection of half-spaces (Figure 13).
To clarify the duality between f(x) and 
, let us drop the
maximum and rewrite the inequality as:
In this equation, the roles of the two functions are interchangeable
and we may suspect that also f(x) can obtained from the dual
function by an optimization procedure. This is in
fact the case and we have:
This equality states that the dual of the dual gives back the original function. It provides the computational tool for calculating dual functions.
For concave (convex down) functions the results are analogous;
we replace 
with 
, and lower bounds with upper bounds.
