| Reconfigurable Computing Seminar | 2/2/98 |
 Slide 1: Systolic Computing February 2, 1998
Slide 1: Systolic Computing February 2, 1998 Slide 2: Talks
Slide 2: Talks Slide 3: Lab 2
Slide 3: Lab 2 Slide 4: PipeRench Tutorial
Slide 4: PipeRench Tutorial Slide 5: Systolic Computing
Slide 5: Systolic Computing Slide 6: Systolic Computing
Slide 6: Systolic Computing Slide 7: Motivation
Slide 7: Motivation Slide 8: Using VLSI Effectively
Slide 8: Using VLSI Effectively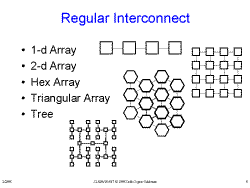 Slide 9: Regular Interconnect
Slide 9: Regular Interconnect Slide 10: Eliminating the VN Bottleneck
Slide 10: Eliminating the VN Bottleneck Slide 11: Balancing I/O and Compute
Slide 11: Balancing I/O and Compute Slide 12: Exploiting Concurrency
Slide 12: Exploiting Concurrency Slide 13: Systolic Architectural Model
Slide 13: Systolic Architectural Model Slide 14: Systolic Is Good RC Starting Point.
Slide 14: Systolic Is Good RC Starting Point. Slide 15: One Big Difference
Slide 15: One Big Difference Slide 16: Mapping Approach
Slide 16: Mapping Approach Slide 17: Various Possible Implementations
Slide 17: Various Possible Implementations Slide 18: Bag of Tricks
Slide 18: Bag of Tricks Slide 19: Bogus Attempt at Systolic FIR
Slide 19: Bogus Attempt at Systolic FIR Slide 20: Bogus Attempt: Outer Loop
Slide 20: Bogus Attempt: Outer Loop Slide 21: Bogus Attempt: Outer Loop-2
Slide 21: Bogus Attempt: Outer Loop-2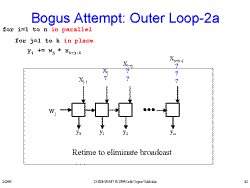 Slide 22: Bogus Attempt: Outer Loop-2a
Slide 22: Bogus Attempt: Outer Loop-2a Slide 23: Bogus Attempt: Outer Loop-3
Slide 23: Bogus Attempt: Outer Loop-3 Slide 24: Attempt at Systolic FIR
Slide 24: Attempt at Systolic FIR Slide 25: Outer Loop
Slide 25: Outer Loop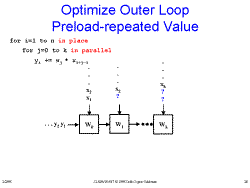 Slide 26: Optimize Outer Loop Preload-repeated Value
Slide 26: Optimize Outer Loop Preload-repeated Value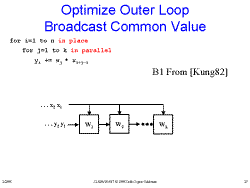 Slide 27: Optimize Outer Loop Broadcast Common Value
Slide 27: Optimize Outer Loop Broadcast Common Value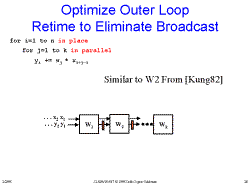 Slide 28: Optimize Outer Loop Retime to Eliminate Broadcast
Slide 28: Optimize Outer Loop Retime to Eliminate Broadcast Slide 29: How It Works
Slide 29: How It Works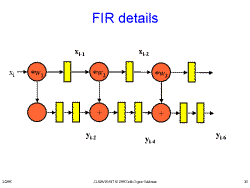 Slide 30: FIR details
Slide 30: FIR details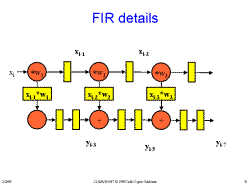 Slide 31: FIR details
Slide 31: FIR details Slide 32: FIR Summary
Slide 32: FIR Summary