A triangular mesh generator rests on the efficiency of its triangulation algorithms and data structures, so I discuss these first. I assume the reader is familiar with Delaunay triangulations, constrained Delaunay triangulations, and the incremental insertion algorithms for constructing them. Consult the survey by Bern and Eppstein [2] for an introduction.
There are many Delaunay triangulation algorithms, some of which are surveyed and evaluated by Fortune [7] and Su and Drysdale [18]. Their results indicate a rough parity in speed among the incremental insertion algorithm of Lawson [11], the divide-and-conquer algorithm of Lee and Schachter [12], and the plane-sweep algorithm of Fortune [6]; however, the implementations they study were written by different people. I believe that Triangle is the first instance in which all three algorithms have been implemented with the same data structures and floating-point tests, by one person who gave roughly equal attention to optimizing each. (Some details of how these implementations were optimized appear in Appendix A.)
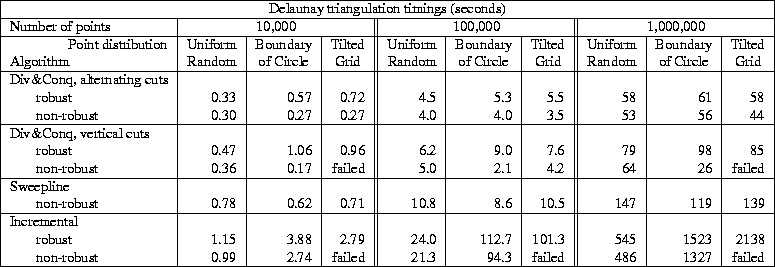
Table 1 compares the algorithms, including versions that use exact arithmetic (see Section 4) to achieve robustness, and versions that use approximate arithmetic and are hence faster but may fail or produce incorrect output. (The robust and non-robust versions are otherwise identical.) As Su and Drysdale [18] also found, the divide-and-conquer algorithm is fastest, with the sweepline algorithm second. The incremental algorithm performs poorly, spending most of its time in point location. (Su and Drysdale produced a better incremental insertion implementation by using bucketing to perform point location, but it still ranks third. Triangle does not use bucketing because it is easily defeated, as discussed in the appendix.) The agreement between my results and those of Su and Drysdale lends support to their ranking of algorithms.
An important optimization to the divide-and-conquer algorithm, adapted from Dwyer [5], is to partition the vertices with alternating horizontal and vertical cuts (Lee and Schachter's algorithm uses only vertical cuts). Alternating cuts speed the algorithm and, when exact arithmetic is disabled, reduce its likelihood of failure. One million points can be triangulated correctly in a minute on a fast workstation.
All three triangulation algorithms are implemented so as to eliminate duplicate input points; if not eliminated, duplicates can cause catastrophic failures. The sweepline algorithm can easily detect duplicate points as they are removed from the event queue (by comparing each with the previous point removed from the queue), and the incremental insertion algorithm can detect a duplicate point after point location. The divide-and-conquer algorithm begins by sorting the points by their x-coordinates, after which duplicates can be detected and removed. This sorting step is a necessary part of the divide-and-conquer algorithm with vertical cuts, but not of the variant with alternating cuts (which must perform a sequence of median-finding operations, alternately by x and y-coordinates). Hence, the timings in Table 1 for divide-and-conquer with alternating cuts could be improved slightly if one could guarantee that no duplicate input points would occur; the initial sorting step would be unnecessary.
Should one choose a data structure that uses a record to represent each edge, or one that uses a record to represent each triangle? Triangle was originally written using Guibas and Stolfi's quad-edge data structure [10] (without the Flip operator), then rewritten using a triangle-based data structure. The quad-edge data structure is popular because it is elegant, because it simultaneously represents a graph and its geometric dual (such as a Delaunay triangulation and the corresponding Voronoï diagram), and because Guibas and Stolfi give detailed pseudocode for implementing the divide-and-conquer and incremental Delaunay algorithms using quad-edges.
Despite the fundamental differences between the data structures, the quad-edge-based and triangle-based implementations of Triangle are both faithful to the Delaunay triangulation algorithms presented by Guibas and Stolfi [10] (I did not implement a quad-edge sweepline algorithm), and hence offer a fair comparison of the data structures. Perhaps the most useful observation of this paper for practitioners is that the divide-and-conquer algorithm, the incremental algorithm, and the Delaunay refinement algorithm for mesh generation were all sped by a factor of two by the triangular data structure. (However, it is worth noting that the code devoted specifically to triangulation is roughly twice as long for the triangular data structure.) A difference so pronounced demands explanation.
First, consider the different storage demands of each data structure,
illustrated in Figure 1.
Each quad-edge record contains four pointers to neighboring quad-edges,
and two pointers to vertices (the endpoints of the edge).
Each triangle record contains three pointers to neighboring triangles,
and three pointers to vertices. Hence, both structures contain
six pointers.![]() A triangulation contains roughly three edges
for every two triangles. Hence, the triangular data structure is
more space-efficient.
A triangulation contains roughly three edges
for every two triangles. Hence, the triangular data structure is
more space-efficient.
It is difficult to ascertain with certainty why the triangular data structure is superior in time as well as space, but one can make educated inferences. When a program makes structural changes to a triangulation, the amount of time used depends in part on the number of pointers that have to be read and written. This amount is smaller for the triangular data structure; more of the connectivity information is implicit in each triangle. Caching is improved by the fact that fewer structures are accessed. (For large triangulations, any two adjoining quad-edges or triangles are unlikely to lie in the same cache line.)
Because the triangle-based divide-and-conquer algorithm proved to be fastest, it is worth exploring in some depth. At first glance, the algorithm and data structure seem incompatible. The divide-and-conquer algorithm recursively halves the input vertices until they are partitioned into subsets of two or three vertices each. Each subset is easily triangulated (yielding an edge, two collinear edges, or a triangle), and the triangulations are merged together to form larger ones. If one uses a degenerate triangle to represent an isolated edge, the resulting code is clumsy because of the need to handle special cases. One might partition the input into subsets of three to five vertices, but this does not help if the points in a subset are collinear.
To preserve the elegance of Guibas and Stolfi's presentation of the divide-and-conquer algorithm, each triangulation is surrounded with a layer of ``ghost'' triangles, one triangle per convex hull edge. The ghost triangles are connected to each other in a ring about a ``vertex at infinity'' (really just a null pointer). A single edge is represented by two ghost triangles, as illustrated in Figure 2.
Ghost triangles are useful for efficiently traversing the convex hull edges during the merge step. Some are transformed into real triangles during this step; two triangulations are sewn together by fitting their ghost triangles together like the teeth of two gears. (Some edge flips are also needed. See Figure 3.) Each merge step creates only two new triangles; one at the bottom and one at the top of the seam. After all the merge steps are done, the ghost triangles are removed and the triangulation is passed on to the next stage of meshing.
Precisely the same data structure, ghost triangles and all, is used in the sweepline implementation to represent the growing triangulation (which often includes dangling edges). Details are omitted.
Augmentations to the data structure are necessary to
support the constrained triangulations needed for mesh generation.
Constrained edges are edges that may not be removed in the process of
improving the quality of a mesh, and hence may not be flipped during
incremental insertion of a vertex.
One or more constrained edges collectively represent an input segment.
Constrained edges may carry additional information, such
as boundary conditions for finite element simulations. (A future version
of Triangle may support curved segments this way.)
The quad-edge structure supports such constraints easily;
each quad-edge is simply
annotated to mark the fact that it is constrained, and perhaps
annotated with extra information.
It is more expensive to represent constraints
with the triangular structure; I augment each
triangle with three extra pointers (one for each edge),
which are usually null but may point to
shell edges, which represent constrained edges and carry additional
information. This eliminates the space advantage of the triangular data
structure, but not its time advantage. Triangle uses the longer record
only if constraints are needed.