Butterfly and dilated butterfly networks belong to a larger class of
networks that are often referred to as splitter networks. The
switches on each level of a splitter network can be partitioned into
blocks. All of the switches on level 0 belong to the same
block. On level 1, there are two blocks, one consisting of the
switches that are in the upper 
rows, and the other consisting of
the switches that are in the lower 
rows. In general, the
switches in a block B of size 
on level l have neighbors
in two blocks, 
and 
, on level l+1, where u stands for
upper and l for lower. The upper block, 
,
contains the switches on level l+1 that are in the same rows as the
upper 
switches of B. The lower block, 
, consists of the
switches that are in the same rows as the lower 
switches of B.
The edges from B to 
are called the up edges, and those
from B to 
are called the down edges. The three
blocks, B, 
, and 
, and the edges between them are
collectively called a splitter. The switches in B are called
the splitter inputs, and those in 
and 
are called the
splitter outputs. In a splitter network with
multiplicity d, each splitter input is incident to d outgoing
up edges and d outgoing down edges, and each splitter output is
incident to 2d incoming edges. In a d-dilated butterfly, the d
up (and d down) edges incident to each splitter input all lead to the
same splitter output, but this need not be the case in general. For
example, we have illustrated an 8-input splitter network with
multiplicity 2 in Figure 2.
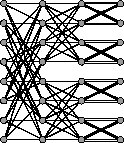
Figure 2: An
8-input splitter network with multiplicity 2.
In a splitter network, each input and output are connected by a single logical (up-down) path through the blocks of the network. For example, Figure 3 shows the logical path from any input to output 011. In a butterfly, this logical path specifies a unique path through the network, since only one up and one down edge emanate from each switch. (In fact, a splitter network with multiplicity one is very similar to a delta network [17].) In a general splitter network with multiplicity d, however, each switch will have d up and d down edges, and each step of the logical path can be taken on any one of d edges. Hence, one logical path can be realized by a myriad of physical paths in a general splitter network.
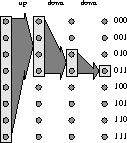
Figure 3: The logical path from any input
to output 011.