This section presents data generated by a PASCAL program that simulates randomly-wired splitter networks. The experimental data demonstrates that a randomly-wired splitter network with multiplicity 2 is capable of routing efficiently even when many of its switches are faulty. The random numbers used in the simulations were generated using the minimal standard linear congruential generator from [24].
The program tested the ability of a randomly-wired splitter network with multiplicity 2 to tolerate randomly-placed faults. Four types of splitter networks were compared: normal butterflies, a 2-dilated butterfly, randomly-wired splitter networks with multiplicity 2, and randomly-wired splitter networks with multiplicity 2 that were modified to improve their fault tolerance. Each network had N=1024 inputs. The randomly-wired networks were ``cleaned up'' after their creation to remove parallel edges between the same two switches where possible.
The program primarily simulated store-and-forward routing. Messages were routed according to a simple greedy algorithm. At each time step, a switch was allowed to send a message along an edge provided that at the end of the previous step the number of messages in the switch at the end of the edge was at most 4. The average number of steps required to route all of the messages to their destinations was measured.
We made two modifications to the random networks in order to make them
more fault tolerant. First, we removed the last 2 levels and
replaced each 4-input splitter on these levels with a 
complete bipartite graph. We then added a level numbered -1 with
4 random matchings to level 0. We use an asterisk (*) in
Tables 1 through 3 to
indicate that the networks were modified.
Faults were placed at random interior (i.e., not input or output)
switches of the modified splitter networks. A non-faulty switch was
declared faulty if either both of its up edges or both of its down
edges led to faulty switches. Thus, faults could propagate from the
last interior level back to the inputs. Because the faults were
placed at random, the modified splitter networks could tolerate about
faults without any faults propagating back to the
inputs. If any faults reached the inputs, then all of the faults were
removed, and a new set of random faults was placed in the network.
The number of faults in the modified splitter networks varied from 0
to 1000. Table 1 shows the percentage of trials
in which at least one fault reached the inputs.
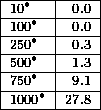
Table 1: Network failure rate. The left column shows the number of
randomly-placed faults. The right column shows the percentage of
trials in which at least one fault was propagated back to an input in
a 1024-input modified randomly-wired splitter network with
multiplicity 2. Each box represents 2000 trials.
We first ran a set of trials to compare the performance of the
randomly-wired splitter networks to the normal butterflies and the
2-dilated butterflies when routing random and worst-case problems. We
ran 4 types of trials. The first type consisted of routing a message
from each input to a random destination, for a total of N=1024
messages. The second consisted of routing a collection of 10 such
random routing problems. The third type was the transpose
permutation, a worst-case problem for the butterfly and dilated
butterfly. In this problem the destination of each message is formed
by rotating the binary representation of the origin of the message
positions in a circular fashion. The last type
consisted of 10 of these transpose permutations. For each of these
types, we varied the number of faults in the modified randomly-wired
splitter networks from 0 to 1000.
The data is presented in Table 2. There is one
column in the table for each type of routing problem: a random problem
(1), 10 random problems (10), a transpose problem (1T), and 10
transpose problems (10T). For each type of network tested, there is a
row in the table. Each entry in a row shows the average, over 500
trials, of the number of steps required to route all of the packets to
their destinations, and the standard deviation, 
. The
butterfly rows are labeled 0 (nor), the 2-dilated butterfly rows are
labeled 0 (dil), the randomly-wired splitter network rows are labeled
0, and the modified randomly-wired splitter network rows are labeled
through 
depending on the number of faults in the
network.
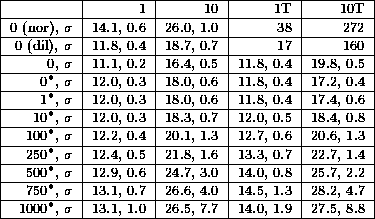
Table 2: Store-and-forward completion time. Each box shows the
average, over 500 trials, of the number of steps for all of the
packets to reach their destinations, and the standard deviation.
Surprisingly, a randomly-wired splitter network with up to 100 faults performs nearly as well as the fault-free 2-dilated butterfly on random problems, and much better on transpose problems, even though both networks consist of the same amount of hardware.
It is also possible to use this program to simulate circuit-switching.
In the circuit-switching model, the goal of a message is to
establish a dedicated path from its source to its destination. This
path must be disjoint from the paths of all other messages; an edge
can appear on at most one message's path. This model is most
appropriate when the messages being transmitted are too long to be
considered atomic objects. For circuit-switching we ran the same
algorithm but instead measured the percentage of messages that reached
their destinations without ever being delayed. These messages can be
viewed as having successfully locked down paths from their sources to
their destinations. The data is presented in
Table 3. Here we found that a modified
randomly-wired splitter network with 100 faults outperformed a
fault-free 2-dilated butterfly! In a related paper [2],
we describe more sophisticated circuit-switching algorithms that
guarantee that all of the messages succeed in establishing their paths
in 
time.
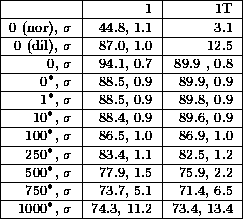
Table 3: Average throughput. Each box shows the average, over 500
trials, percentage of messages that successfully locked down their
paths, and the standard deviation.
Additional experimental data on the performance of randomly-wired splitter networks can be found in [4, 5, 13, 15, 21].