We will analyze the behavior of the greedy algorithm described in
Section 2.1 by means of a potential function argument.
In particular, we will assign each packet in wave i 
weight 
for some fixed 
to be determined
later, and we will define the potential of a switch on level
k 
to be 
if k is odd, and 
if k is even,
where w < 1 is also a constant to be determined later. Thus, the
potential of a packet in the ith wave at the kth level is
if k is odd, and 
if k is even, and the
potential of the system is the sum of potentials of the
packets. By varying the values of 
and w, we can obtain
different bounds on the running time of the algorithm as follows.
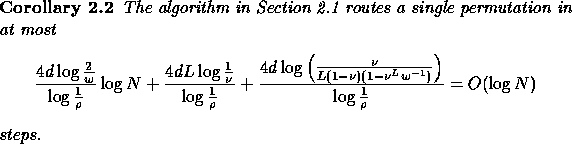
The key fact necessary to prove Theorem 2.1 is that the potential of the system drops by a constant fraction during each stage. In particular, we will need to prove the following claim.
The main idea behind proving Claim 2.4 is that during any stage of the algorithm, a reasonable number of the heaviest packets move forward, thereby decreasing the potential of the system by a constant fraction. To formalize this intuition, we will need the following series of lemmas.
Proof: Consider any edge e. At some step of the phase, the algorithm looks at the head and tail of e, and rearranges packets (if any) so that the heavier weight packet is sent to the head of e. In subsequent steps, only a packet with greater weight can be moved into the head of e, and only packets with lesser weight can move into the tail of e. Hence at the end of the phase, the weight of the packet at the head of e is at least as great as the weight of the packet at the tail of e, if any. (Nonexistent packets can be considered to have zero weight.)
In what follows, let 
denote the sum of the weights of the
r heaviest upward-destined packets left at the inputs of a splitter
after a phase of routing through the splitter. If there are fewer
than r upward-destined packets left at the inputs, then 
denotes the weight of all of them. A similar definition holds for
and also for 
and 
, which denote the
sum of the weights of the r heaviest packets in the upper and lower
outputs, respectively.
Proof: For simplicity, we will only argue the result for upward destined packets. The proof for lower-destined packets is identical.
We will prove by induction on r that 
. For r=1, the
result follows from Lemma 2.5 and the fact that every input
is adjacent to 
upper outputs. Now assume the result is
true for r=k-1, and look at the k heaviest upward-destined packets
left at the inputs of the splitter. By the expansion property, we
know that the inputs containing these packets are incident to at least
upper outputs. By Lemma 2.5, each
of these outputs contains a packet of weight at least
(i.e., the weight of the kth heaviest
upper-destined packet left at an input). Hence, there are 
or more upper outputs containing packets with weight
at least 
, and by induction, the 
heaviest of these account for at least 
weight.
Thus,
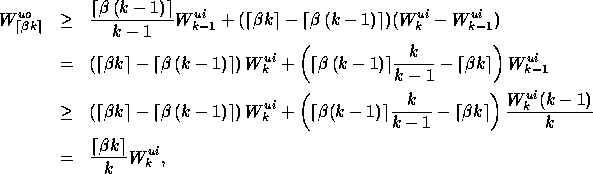
thereby verifying the inductive hypothesis.
Proof:
For simplicity, we will only consider upward-destined
packets. The same argument holds for lower-destined packets. Arrange
the packets at the inputs in order of decreasing weight. Since
, at most 
of these packets can belong to any wave. Hence the weight of
the 
th heaviest packet is at most
times the weight of the ith heaviest packet for all i.
Since the weight of the 
heaviest packets is
by definition, the total weight of
all the upper-destined packets at the inputs is at most
as claimed.
Proof:
By Lemma 2.6, the total weight of
packets on the upper and lower outputs is at least 
. By
Lemma 2.7, the total weight of packets left at the
inputs is at most 
. Hence the total weight on the
outputs is at least 
times the total weight on the
inputs, and thus at least a 
fraction of the weight is on the outputs.
We are now ready to prove Claim 2.4 and Theorem 2.1.
Proof of Claim 2.4: Let 
denote
the weight at the beginning of the stage in levels l and l+1,
where l is even. If V is the potential of the system at the
beginning of the stage, then
During the first phase of the stage, packets move from even levels to
odd levels. This does not change the potential of the system since
each even level has the same potential as the next odd level. However,
it does ensure that the weight in odd level l+1 is at least 
and the weight in even level l is at most 
.
During the second phase, the weight in odd level l+1 is rearranged
with the weight in even level l+2 for each l. By Corollary 2.9,
and the argument of the previous paragraph, we know that at least
weight moves from level l+1 to
level l+2 for any l. Hence, the potential at the end of the stage
is at most
as claimed.
Proof of Theorem 2.1: To compute an upper
bound on the running time of the algorithm, we now need only to
compute the initial potential of the system and the potential at which
we will be guaranteed that every packet has reached its destination at
level 
.
To compute the initial potential, we will assume without loss of generality that the first L waves start in level 0, the next L waves start in level -1, and so forth. The total weight in the first L waves is at most
Similarly the weight of the
ith group ( 
of L waves is at most
Hence the total initial potential is at most
The potential of a packet from the last wave on level 
is at most 
. Hence, all of the packets must
have reached level 
(their destinations) once the total
potential falls below this amount. Since the total potential drops by
a factor of 
at every stage, the total number of stages can be
at most S, where
Hence, it suffices to choose
Since each stage takes 4d steps, we can multiply by 4d to obtain the bounded stated in the theorem.
In order to show that 
, we need to show that there
exist constants d, 
, 
, w < 1, and 
such
that 
and 
. The key, of course, is showing
that 
(i.e., that the potential of the system drops during
every stage). If 
, then we can always find a value of
w < 1 for which 
. (In particular, we can choose 
, for then 
.) In order for 
to be greater than 
, it suffices that
. This can be accomplished for any 
by
setting 
to be sufficiently small. Making 
small also
guarantees that 
. Hence, we only need to choose d,
, and 
so that 
, which can be done for any
by choosing 
to be sufficiently small.
For example, we could choose d=11, 
, 
, L
= 16, 
, 
, 
, and 
, to show that 
permutations can be routed in at most
steps using the algorithm.
