Our first algorithm extends the paths from level 0 to level 
by first extending all the paths from level 0 to level 1, then
from level 1 to level 2, and so on. As we shall see, extending
the paths from one level to the next can be done in 
bit
steps, so the total time is 
bit steps.
In a multibutterfly with the 
unshared-neighbors
property, it is relatively easy to extend paths from one level to the
next because paths at nodes with unshared neighbors can be extended
without worrying about blocking any other paths that are trying to
reach the next level. The remaining paths can then be extended
recursively. In particular, all the paths can be extended from
level l to level l+1 (for any l), by performing
a series of ``steps'', where each step consists of:
Note that each step can be implemented in a constant number of bit steps.
Since the splitters connecting level l to level l+1 have 
inputs, and at most 
paths must be extended to the upper (or
lower) outputs, for 
, the number of inputs containing
these paths is at most 
. Thus, we can apply the
unshared-neighbors property to these nodes. As a
consequence, in each step the number of paths still remaining to be
extended decreases by a 
factor. After 
steps, no paths remain to be extended.
By using the path-extension algorithm just described to extend all of the paths from level 0 to level 1, then all of the paths from level 1 to level 2, and so on, we can construct all the paths in
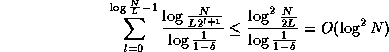
steps.