Our circuit-switching algorithm requires the splitters in the multibutterfly to have a special ``unshared-neighbors'' property defined as follows.
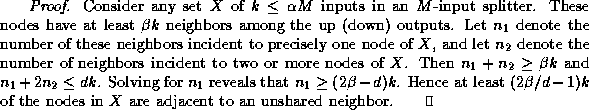
By Equation 2.1, we know that randomly-generated
splitters have the 
unshared-neighbors property where
approaches 1 as d gets large and 
gets small.
Explicit constructions of such splitters are not known, however.
Nevertheless, we will consider only multibutterflies with the
unshared-neighbors property for 
in what
follows.
Remark: The 
expansion property
( 
) is a sufficient condition for the unshared-neighbors
property, but by no means necessary. In fact, we can easily prove the
existence of random splitters which have a fairly strong
unshared-neighbors property for small degree. For
such graphs, the routing algorithm we are about to describe is more
efficient in terms of hardware required. However, multibutterflies
with expansion properties will remain the object of our focus.
