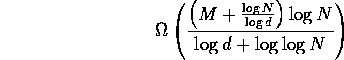
In this section we prove that any randomized oblivious routing algorithm takes
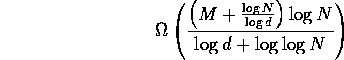
bit steps with high
probability for almost all permutations, where M is the minimum
packet size not including addressing information, N is the size of
the network and d is the maximum degree of the network. The proof
is similar to the classic Borodin-Hopcroft lower bound proof
[7] but extends their method and result in two ways.
First, the lower bound applies to almost all permutations, and second,
it applies to a wider class of algorithms: randomized oblivious
algorithms as opposed to deterministic oblivious algorithms. Our only
assumption is that each packet has at least 
bits of
addressing information if it is still a distance 
away from
its destination. Without this assumption, the lower bound is
bit steps.
Let us first define the notion of a randomized oblivious routing
algorithm. We shall assume that our network is a directed graph
, where |V|=N and the in-degree and out-degree of every
node is at most d. Let p denote a sequence of edges which form a
path (not necessarily simple) in the graph; let 
be the set
of all paths from u to v. For a given randomized routing
algorithm let 
be the random variable denoting the
path from u to v chosen by the algorithm. Using this notation,
for any node or edge x and for all nodes u and v we have the
following:
and
A randomized oblivious routing algorithm is one
in which all distinct random variables 
are
independent.
We should discuss how the definition of obliviousness applies to
networks which have multiple edges. We consider each edge of a bundle
of multiple edges to be distinct so that paths which use different
edges in the same bundle are considered to be different. This implies
that oblivious algorithms on networks with multiple edges must be
oblivious to the choice of edges within bundles of edges. Hence, even
though our routing algorithm for the dilated butterfly chooses the
nodes along a packet's path obliviously, it is not an oblivious
algorithm because the choices of edges within a bundle depended upon
the choices made by other packets. This is what allows us to achieve
bit steps and beat the lower bound.
Networks where edges have capacity c (and degree 
) are
considered to be networks with multiple edges and degree 
.
Hence, for an N node hypercube with capacity 
on its edges,
i.e., 
, we find that any randomized oblivious algorithm
takes 
bit steps
with high probability, even if 
. In fact, messages typically
have length 
. For 
, the bound
is 
. More generally, if 
, the bound is 
.
Given a randomized oblivious routing algorithm for a network we would like a measure of how likely it is for a node or edge to be in a randomly selected set of paths. For any node v, any set of nodes T, and any node or edge x, we define the weight of x with respect to v and T to be
Note that the weight of a node is equal to the sum of the weights of its incoming (or outgoing) edges.
Observe that if we choose a random destination 
and a random
path from v to t according to the 
, then x will
be contained in the path with probability
. Similarly, if we choose a random path
from v to a randomly selected destination in V, then x will be
contained in the path with probability at least
.
The goal of the proof is to show that there are many edges e that
have many nodes v for which 
is large for some
T. Then we will be able to argue that many edges have at least
some chance of having many packets pass through them. (We will also
argue that these packets still have a long way to go after using the edge
in order to show that many bits are likely to pass through the
edge.) Then we will conclude that at least one of these
edges has high congestion with very high probability.
We start by proving that for any node v and any large set T, there
are many pairs 
for which 
is
large
and u is far away from 
. Henceforth, we use the notation
to denote the minimum distance between
x and any element of T in the graph.
Proof:
Consider the set of nodes
where 
.
Observe that 
is a lower bound for 
,
since 
and
for all t. Now we will derive
an upper bound for 
in terms of |U|. This in turn will
imply a lower bound for |U|. By
definition,
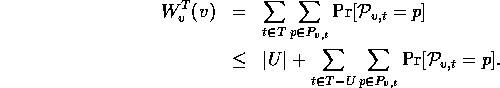
Observe that 
. For any path in the preceding sum from v
to a node in T-U let y be the first node not in U and let
Y be the set of all y. We can partition the paths according to
Y as follows:
This is bounded by
since the size of Y is at most d|U| and the
weight of any node not in U is at most k.
Thus,
Combining the two inequalities for 
reveals that
.
For each 
, define 
to be the subset of nodes in T that
are not within distance 
of u. Since the maximum node degree is d,
there are at most 
nodes within distance h of a node.
Hence, there are at most 
nodes within distance
of u, and thus
The above lemma allows us to show that there is an edge with large weight.
Proof:
By Lemma 4.1 and the fact that 
, we
know that there are 
pairs of nodes 
, where 
,
and each pair has an associated subset 
such that
and 
Recall that the weight of a node is equal to the sum of the
weights of its incoming edges and that
every node has maximum in-degree d. Hence, there
are at least 
node-edge pairs 
for which
, 
, 
, and 
.
Since there are at most dN edges, we can therefore conclude that
there is at least one edge e for which there are at least
nodes 
for which 
, 
, and 
.
We are now ready to prove the lower bound on randomized oblivious algorithms.
Proof:
We will show that for a random permutation, the probability
that every edge has fewer than 
packets passing through it that are 
steps away
from their destination is at most 
for a sufficiently
small constant c. In this case, the probability is taken over the
choice of permutations as well as the choice of paths. This directly
implies the theorem since if more than an 
fraction of
the possible permutations finished in fewer than 
bit steps with probability
exceeding 
, then we would have more than a
chance of finishing in fewer steps with a random
permutation which is not possible.
We will construct the random permutation by determining one path at a time.
We will randomly select a path for each node v in a specified sequence,
selecting paths from the distributions for 
where u is
randomly selected from the nodes not already designated to receive a packet.
(The constraint of constructing a random permutation rather than
a random destination requires that at most one packet be delivered to
any node. The argument for random destinations is somewhat easier.)
We start by selecting an edge e and 
nodes
, where S=T=V, such that for 
,
where 
and 
.
Such an edge and set of nodes is guaranteed to exist by
Lemma 4.2. We first select a random destination 
from
and a random path 
from 
for 
. Since
,
we know that
the path 
contains e and continues afterward for at least
steps with probability at least
.
We next select a random destination 
from 
and a random
path 
from 
for 
. Since
we know that 
uses e and continues afterward for at least
steps with probability at least
. Moreover, we know that this probability is independent
of the probability that 
uses e and
continues afterward for 
steps.
Arguing in a similar fashion, we can show that 
each use e and continue afterward for at least 
steps with probability 
, and that
these probabilities are independent. Since there are 
paths, each using e and continuing afterwards for 
steps with probability 
,
the probability that at least
paths use e and continue afterwards for 
steps
is at least
for some constant 
and sufficiently large N.
By selecting c to be a small enough constant, this
probability can be made to be at least 
. In other words, at least
bits
pass through e from packets starting at nodes
with probability at least 
.
We now start over again, setting 
and
. Since 
,
, and we can apply Lemma 4.2 to
find an edge 
and nodes 
such that for 
where 
and
. Arguing
just as before (except that now 
is selected uniformly from
)
we can prove that at
least
bits
pass through 
from packets starting at nodes
with probability at least 
.
We can repeat this whole process 
times before violating our condition that S and
T have more than 
nodes.
Each repetition we select destinations and paths for m more
nodes. Each time we severely congest an edge with probability at least
. Since these probabilities are all independent, the
probability that none of the edges is severely congested is at most
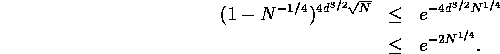
Hence for a random permutation and random path selection, the running
time will be 
with
probability 
.
