Our sparse matrix multiplication code for the Cray Y-MP family (written in Cray assembly language) is publicly available.
function MxV(Mval, Midx, Mlen, Vect) =
let v = Vect -> Midx;
p = {a * b: a in Mval; b in v}
in
{sum(row) : row in nest(p, Mlen)};
In this example, Mval contains the non-zero matrix values in a
compressed row format, Midx contains the column index of each
non-zero element, and Mlen contains the number of non-zero elements
in each row. For details about the implementation and performance of this
NESL code, see our paper,
Implementation
of a Portable Nested Data-Parallel Language. For a longer example
of NESL sparse matrix code, see our implementation of the
Conjugate
Gradient algorithm.
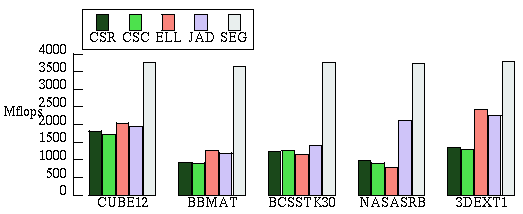
Sparse Matrix Multiplication on Vector Multiprocessors:
The NAS
benchmark report includes timings of our Cray Y-MP/C90
implementation of the Conjugate Gradient benchmark. Our implementation
is currently the fastest reported for any machine. In our paper,
Segmented
Operations for Sparse Matrix Computation on Vector Multiprocessors
by Guy Blelloch, Mike Heroux (at Cray
Research), and Marco Zagha, we present a new technique for sparse matrix
multiplication on vector multiprocessors based on a fully vectorized and
parallelized segmented sum algorithm. Because of our method's
insensitivity to relative row size, it is better suited than the
Ellpack/Itpack or the Jagged Diagonal algorithms for matrices which have a
varying number of non-zero elements in each row. Furthermore, our approach
requires less preprocessing, less auxiliary storage, and uses a more
convenient data representation (an augmented form of the standard compressed
sparse row format). On a test suite of sparse matrices from the
Harwell-Boeing collection and industrial application codes, our Cray Y-MP C90
implementation performs up to 3 times faster than the Jagged Diagonal
algorithm and up to 5 times faster than Ellpack/Itpack method. Here is a
summary of our results for 5 test matrices on a 16-processor C90 comparing our
algorithm (SEG) to several other algorithms:

Our
sparse
matrix multiplication code for the Cray Y-MP family (written in Cray
assembly language) is publicly available.
Related Work: Also see our Graph Separators page for more information about implementing finite element computation on distributed memory machines.
Up to the Irregular Algorithms page.