Exercise 6: Breakout, Part I

Before you start this exercise, go over Chapters 11 and 12 to learn about defining new classes.

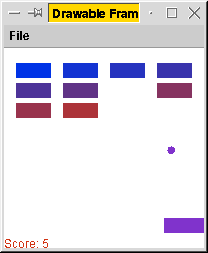In this exercise, we'll develop a program that animates a ball bouncing around a window. In Exercise 7, we will extend this work to form a Breakout game. (The arcade version was branded Arkanoid.) At right is a screen shot of the game we're working toward. But that's a long way from us right now.

In this exercise, we'll just write a program in which a ball bounces around a window containing a single block. Our program for this exercise is divided between three classes: BallTest to handle the overall program, Ball to represent the moving ball, and Block to represent a rectangular obstacle.

Part A. Setting up

Download the updated pgss library from the Web page. It includes several new classes written for Exercises 6 and 7.

In this exercise, you'll be using the documentation for these new classes quite a bit.
Download BallTest.java and insert it into your project. You do this the same way you insert pgss.jar into the project, except that this time you should have the Source Files (not Library Files) option selected.

The BallTest class defines the main() method for the overall program. None of your code should appear in this file - it exists solely so that you can test the classes that you develop in this exercise to ensure they operate as they ought.

The run() method of BallTest works on the same principle as animated movies work: It repeatedly draws what the world is like, then waits for a short while before drawing what the world is like after that wait. If done at a quick enough rate, the human eye is unable to discern the individual still images. In animation terms, each of these drawings is a frame. The BallTest class works at a frame rate of roughly 50 frames a second. (The standard for wide-distribution films is 24 frames per second.)

The main() method uses a Ball object to track its understanding of the world, calling its step() method to step it forward one frame and its draw() method to draw the ball into the current frame.

There are no modifications necessary for this file at this time. (When you reach Part C, you will uncomment four lines in order to test the Block class.)
Designate the BallTest class as your main class, following the instructions on the supplemental Eclipse instruction page.

Part B. The class `Ball`

Now we will write the Ball class, which BallTest uses. The supplemental Eclipse instruction page describes how to insert a new, empty file into your project.

An object of the Ball class represents a ball moving within a window. Such an object will track the ball's location, direction, and velocity. The constructor is as follows.

Ball(int in_left, int in_top, double in_vel, double in_ang): Creates a ball whose left side is at in_left and top side is at in_top. The ball's initial velocity is in_vel, at a direction of in_ang radians.

You'll want to remember the ball's location with doubles so that the ball moves smoothly. (If you remember and compute locations with integers, the round-off errors will result in an unacceptably hideous approximation of what would happen in reality.) Since the graphics routines work with integers, however, we'll often need to round to integers; the Convert.toInt() method (documented in the library documentation) can accomplish this.

Ball should also define a constant DIAMETER to represent the ball's diameter. (A good value is 8.) You should use the constant whenever applicable, never the actual number. This will allow you to easily change the ball's size with no modifications to the rest of your program.

Elementary instance methods

The Ball class will include many instance methods, beginning with the following.

int getTop(): Returns the integer y-coordinate of ball's top.
int getBottom(): Returns the integer y-coordinate of ball's bottom.
int getLeft(): Returns the integer x-coordinate of ball's left side.
int getRight(): Returns the integer x-coordinate of ball's right side.
void draw(Graphics g): Draws the ball at current location using g. It should draw the ball as a solid, colored circle.

It's important to remember that in Java (as in most windowing systems), the upper left corner is (0,0), with coordinates increasing to the right and downward.

In the draw() method, you'll want to refer to the documentation for the Graphics class, part of the java.awt package. (That means that you'll want to include the line ``import java.awt.*; at the top of your file.) You'll want to use its setColor() method in order to set the current color. (See the constants defined in the Color class to find a Color object to pass as a parameter.) And you'll want to use its fillOval() method to actually draw the circle.

Instance methods for bouncing

The remaining methods are more complex, requiring some elementary physics and trigonometry. Of these, the first four handle bouncing the ball in various directions.

void bounceDown(int y): Reflects ball downward from a horizontal line with y-coordinate y.
void bounceUp(int y): Reflects ball upward from a horizontal line with y-coordinate y.
void bounceLeft(int x): Reflects ball leftward from a vertical line with x-coordinate x.
void bounceRight(int x): Reflects ball rightward from a vertical line with x-coordinate x.

These methods would be called in the following situation. For each frame of the animation, your program will step the ball forward one discrete step. Consider the following diagram.

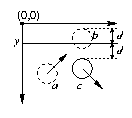The ball was at position a in the previous animation frame, but then the program stepped it forward to position b. The program would detect that the ball has crossed the line at y, and so it would call bounceDown(y) to tell the Ball object to bounce downward off the line.

The bounceDown() method accomplishes two things.

It alters the ball's direction. If the direction was theta before the bounce, it changes to 0-theta (or, when bouncing off a vertical line, pi-theta).
It repositions the ball to the location where it would be if it bounced off the line properly. That is, insofar as the ball crossed the line (the distance between the ball's top and the line, represented as d in the figure), the ball's top is moved below the line (also a distance of d). This repositions the ball at location c in the picture.

Bouncing in the other directions involves analogous thinking. Each of these bouncing methods will look very simple, but you have to think through the mathematics carefully to write them.

Instance method for stepping time

The final method steps the ball forward one step.

void step(GraphicsWindow window): Moves ball one time step, bouncing off the borders of f if applicable.

To do this, you'll want to move the ball forward one time step, according to the current velocity v and direction theta.

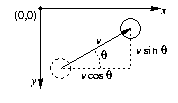After it steps forward, you can determine whether it has crossed any boundaries of the window. If it has, then you should call one of Ball's bouncing methods to bounce it back into the window. (Use the getWidth() and getHeight() methods of the GraphicsWindow class to determine the borders of the window.)

You can find the sine and cosine of an angle represented in radians via the sin and cos class methods of the Math class. (Page 116 of the textbook documents these methods.)

Part C. The class `Block`

Write the Block class to represent a fixed rectangular object off of which the ball can bounce. The constructor for this object is the following.

Block(int in_left, int in_top, int in_width, int in_height): Creates a rectangular block whose top left corner is at the coordinates (in_left,in_top), and which is in_width pixels wide and in_height pixels tall.

The class should support two instance methods.

boolean bounce(Ball b): Bounces b off the block's walls if any piece of b is inside the block, returning true if this occurs.¹
void draw(Graphics g): Draws the block as a solid, colored rectangle using g.

The BouncingBallWindow class includes four commented lines labeled ``//PART C:'' that you can uncomment to test your solution for this part of the exercise.

On to Exercise 7: Breakout, Part II.

¹ Don't worry about the exact details of how things work at the corners of the box - it should just reflect well when it hits the sides squarely in the middle.

If you want it to look good at the corners, I would recommend that you detect that the ball has crossed the lower border when the x-coordinate of the ball's center is between the left and right sides of the block, and of course if the ball has crossed the y-coordinate of the block's lower side. The other sides are analogous.

In the physical world, the interaction at the corners is much more complex, analogous to how billiard balls interact. But deriving such formulas is beyond the scope of this exercise - and, indeed, not something that typical Breakout games do anyway.