 |
Compiling for ASH |
 |
|
|
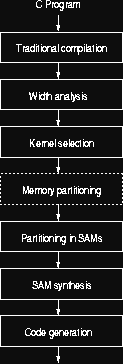
We have developed the CASH (Compiler for ASH) compiler which translates programs written in C into hardware implementations. The compiler applies several code transformations:
- It performs traditional software optimizations.
- We have developed a width analysis algorithm which can discover narrow width computations in C programs. 30% of the bits computed in average C programs are simply useless; in a reconfigurable hardware implementation we can optimize these away.
 - The program is decomposed into parts which are run on the reconfigurable fabric and on the supporting CPU; the CPU will handle tasks which do not map well on the reconfigurable hardware, like virtual memory management, operating system activity and I/O.
- The program is analyzed and the memory used is partitioned into blocks which can be accessed in parallel. If a block is accessed only from a small portion of the computation, it will be laid out close to the circuits accessing it (we haven't implemented this part yet).
- The program is decomposed in SAMs.
- Each SAM is synthesized in hardware.
|
 |
|
|
 |
|
 |
|
 |
 |
Energy Efficiency |
 |
|
|
When implemented directly in hardware, ASH is up to
three orders of magnitude more power-efficient
than superscalar processors, one to two orders of
magnitude better than low-power DSP processors, one order
of magnitude better than asynchronous processors; it is
roughly comparable to compared to custom hand-designed
hardware.
 |
|
 |
|
 |
|
 |
|