
h=.5 - h too big
I illustrate shooting methods, finite difference methods, and the collocation and Galerkin finite element methods to solve a particular ordinary differential equation boundary value problem.
This can be solved analytically; exact motion is quadratic in t, final answer is y'(0)=32.5 [m/sec].

h=.5 - h too big

h=.1 - smaller h gives more accurate results.
But note that the y'(0) that secant method solves for, in red,
is still not correct
(not 32.5), because of errors of our IVP solution.
If we used Runge-Kutta or other more accurate IVP solution method, instead
of Euler's method, that would help.
Below is my Matlab code for the shooting method.
function y = rocket(dy0)
% return altitude at t=te (y(te)) as a function of initial velocity (y'(0)=dy0)
global h te
[tv,yv] = euler2(h,0,te,0,dy0);
plot(tv,yv,'o-', 'LineWidth',2);
% invariant: tv(te/h+1)==te
y = yv(te/h+1); % returns y at t=te
return;
function [tv,yv] = euler2(h,t0,tmax,y0,dy0)
% use Euler's method to solve 2nd order ODE y''=-g+a*y^2
% return tvec and yvec sampled at t=(t0:h:tmax) as col. vectors
% y(t0)=y0, y'(t0)=dy0
% Paul Heckbert 30 Oct 2000
global a; % coeff of nonlinear acceleration
g = 9.8; % accel. of gravity, [m/sec^2]
y = y0; % position
dy = dy0; % velocity
tv = [t0];
yv = [y0];
for t = t0:h:tmax
y = y+dy*h; % this and following line are Euler's method
dy = dy+(-g+a*y^2)*h;
tv = [tv; t+h];
yv = [yv; y];
end
return;
function ret = shoot(hh)
% shooting method for fireworks problem
global a te ye h;
a = 0; % coeff of nonlinear acceleration
te = 5; % end time [sec]
ye = 40; % end height [m]
h = hh;
clf;
hold on;
for dy = 20:10:50
y = rocket(dy);
text(te+.2,y,sprintf('y\047(0)=%g',dy), 'FontSize',15);
end
% now use root finding to find correct initial velocity
dy = secant(20,30,1e-4);
% draw last curve
y = rocket(dy);
text(te+.2,y,sprintf('y\047(0)=%g',dy), 'Color','r', 'FontSize',15);
set(gca, 'FontSize', 16); % for tick marks
line([te te],[-40 140], 'Color','k');
line([te te],[ye ye], 'Color','r', 'Marker','o', 'LineWidth',3);
xlabel('t', 'FontSize',20);
ylabel('y', 'FontSize',20);
title(sprintf('Shooting Method on y\047\047=-g'), 'FontSize',20);
return;
function x = secant(x1,x2,tol)
% secant method for one-dimensional root finding
global ye;
y1 = rocket(x1)-ye;
y2 = rocket(x2)-ye;
while abs(x2-x1)>tol
disp(sprintf('(%g,%g) (%g,%g)', x1, y1, x2, y2));
x3 = x2-y2*(x2-x1)/(y2-y1);
y3 = rocket(x3)-ye;
x1 = x2;
y1 = y2;
x2 = x3;
y2 = y3;
end
x = x2;
return;

When we do shooting method we find roots of this function.
For this particular, very simple, problem the function is linear,
so root finding is trivial (secant method converges in one iteration).
In general, the root-finding problem is linear if the
differential equation is linear.
Above plot is made like so:
function rocketplot
% plot the function which we're finding roots of, in shooting method
global a;
a = 0; % coeff of nonlinear acceleration
hold off;
yv = [];
dy0v = 20:5:50;
for dy0 = dy0v
y = rocket(dy0);
yv = [yv y];
end
set(gca, 'FontSize', 16); % for tick marks
plot(dy0v,yv, '-', 'LineWidth',2);
xlabel('initial velocity', 'FontSize',20);
ylabel('y(5) = altitude at t=5', 'FontSize',20);
title(sprintf('Root-Finding Problem for Shooting Method on y\047\047=-g'), 'FontSize',16);
line([20 50], [40 40], 'Color','k');
Now let's temporarily look at a different problem, y''=-g+.01*y^2, which is nonlinear. (I know of no reasonable physical basis for this ODE; it's cooked up.)

Trajectories are no longer parabolas.

And makes this function nonlinear, so root finder has to do more work
(takes about 5 iterations).
This ODE was solved with code just like shoot.m, shown earlier, except a=.01 .
Now we go back to original problem, y''=-g.

With n=10 intervals and n+1=11 function samples.
We end up solving an 11x11 tridiagonal system.
Can be done in time linear in n.
function findif(n)
% finite differences method to solve fireworks problem
% n is number of divisions
global g te ye h;
g = 9.8; % accel. of gravity, [m/sec^2]
te = 5; % end time [sec]
ye = 40; % end height [m]
h = te/n;
A(1,1) = 1;
b(1) = 0; % y0 = 0
for i = 2:n
A(i, i-1:i+1) = [1 -2 1];
b(i) = -g*h^2;
end
A(n+1,n+1) = 1;
b(n+1) = ye;
b = b'; % make b into a column vector
y = A\b;
A
b'
y'
(y(2)-y(1))/h
(4*y(2)-y(3))/(2*h) % best est. of initial velocity (parab thru 1st 3 pts)
hold off;
set(gca, 'FontSize', 16); % for tick marks
plot(0:h:te, y, 'bo-', 'LineWidth',2);
xlabel('t', 'FontSize',20);
ylabel('y', 'FontSize',20);
title('Finite Difference Method', 'FontSize',20);
Here is what the above code prints out.
>> findif(10)
A =
1 0 0 0 0 0 0 0 0 0 0
1 -2 1 0 0 0 0 0 0 0 0
0 1 -2 1 0 0 0 0 0 0 0
0 0 1 -2 1 0 0 0 0 0 0
0 0 0 1 -2 1 0 0 0 0 0
0 0 0 0 1 -2 1 0 0 0 0
0 0 0 0 0 1 -2 1 0 0 0
0 0 0 0 0 0 1 -2 1 0 0
0 0 0 0 0 0 0 1 -2 1 0
0 0 0 0 0 0 0 0 1 -2 1
0 0 0 0 0 0 0 0 0 0 1
b =
Columns 1 through 7
0 -2.4500 -2.4500 -2.4500 -2.4500 -2.4500 -2.4500
Columns 8 through 11
-2.4500 -2.4500 -2.4500 40.0000
y =
Columns 1 through 7
0 15.0250 27.6000 37.7250 45.4000 50.6250 53.4000
Columns 8 through 11
53.7250 51.6000 47.0250 40.0000
ans =
30.0500 linear est. of initial velocity
ans =
32.5000 quadratic est. of initial velocity
Note that the second estimate of launch velocity above is exact.

Blue: solution u(t); Red: scaled basis functions u[i]*phi[i](t) for i=1..n+2.
With n=4 interior intervals and n+2=6 basis functions.
We end up solving a 6x6 tridiagonal system.
Can be done in time linear in n.
Because the correct solution is quadratic, and our basis functions span the space of all quadratic functions, collocation computes an exact solution to this problem, even when n=1.
function colloc(n)
% collocation finite element method to solve fireworks problem
% n is number of divisions
% using quadratic B-spline basis functions
global g te ye h;
g = 9.8; % accel. of gravity, [m/sec^2]
te = 5; % end time [sec]
ye = 40; % end height [m]
h = te/n;
A(1, 1:2) = [1/2 1/2];
b(1) = 0; % y=0 at t=0
for i = 2:n+1
A(i, i-1:i+1) = [1 -2 1];
b(i) = -g*h^2;
end
A(n+2, n+1:n+2) = [1/2 1/2];
b(n+2) = ye; % y=ye at t=te
b = b'; % make b into a column vector
u = A\b;
A
b'
u'
(u(2)-u(1))/h % initial velocity
% plot(-h/2:h:te+h/2, u, 'g'); % plot the coefficients
tv = 0:h/8:te; % supersample the parabolas
yv = [];
for t = tv
i = floor(t/h)+2;
if i==n+2
i = n+1;
end
x = t/h-i+1.5;
y = u(i-1)*.5*(x-.5)^2 + u(i)*(.75-x^2) + u(i+1)*.5*(x+.5)^2;
yv = [yv y];
end
% compute joints between elements
tk = (0:h:te)';
yk = .5*(u(1:n+1)+u(2:n+2));
clf;
hold on;
set(gca, 'FontSize', 16); % for tick marks
plot(tv,yv,'b', tk,yk,'bo', 'LineWidth',2);
xlabel('t', 'FontSize',20);
ylabel('y', 'FontSize',20);
title('Collocation Finite Element Method', 'FontSize',20);
% draw scaled basis functions
dh = h/15;
eps = 1e-5;
for i = 1:n+2
tv1 = (i-3)*h:dh:(i-2)*h-eps;
yv1 = u(i)*.5*(tv1/h-i+3).^2;
tv2 = (i-2)*h:dh:(i-1)*h-eps;
yv2 = u(i)*(.75-(tv2/h-i+1.5).^2);
tv3 = (i-1)*h:dh:i*h+eps;
yv3 = u(i)*.5*(tv3/h-i).^2;
plot([tv1 tv2 tv3], [yv1 yv2 yv3], 'r', 'LineWidth',2);
end
hold off;
Here is what the above code prints out:
>> colloc(4)
A =
0.5000 0.5000 0 0 0 0
1.0000 -2.0000 1.0000 0 0 0
0 1.0000 -2.0000 1.0000 0 0
0 0 1.0000 -2.0000 1.0000 0
0 0 0 1.0000 -2.0000 1.0000
0 0 0 0 0.5000 0.5000
b =
0 -15.3125 -15.3125 -15.3125 -15.3125 40.0000
u =
-20.3125 20.3125 45.6250 55.6250 50.3125 29.6875
ans =
32.5000
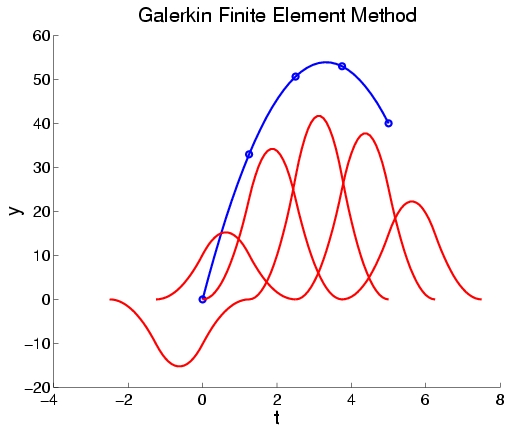
Blue: solution u(t); Red: scaled basis functions u[i]*phi[i](t) for i=1..n+2.
With n=4 interior intervals and n+2=6 basis functions.
We end up solving a 6x6 pentadiagonal system.
Can be done in time linear in n.
Note that solution is exactly the same as with collocation method, for this particular problem, and is an exact solution, but that's not true in general. We could also solve this problem exactly with n=1 using these basis functions.
function galerkin(n)
% Galerkin finite element method to solve fireworks problem
% n is number of divisions
% using quadratic B-spline basis functions
global g te ye h;
g = 9.8; % accel. of gravity, [m/sec^2]
te = 5; % end time [sec]
ye = 40; % end height [m]
h = te/n;
A(1, 1:2) = [.5 .5];
b(1) = 0; % y=0 at t=0
A(2, 1:4) = [4 -7 2 1]; % Galerkin condition on first interior intvl
b(2) = -5*g*h^2;
for i = 3:n
A(i, i-2:i+2) = [1 2 -6 2 1];
b(i) = -6*g*h^2;
end
A(n+1, n-1:n+2) = [1 2 -7 4]; % last interior interval
b(n+1) = -5*g*h^2;
A(n+2, n+1:n+2) = [.5 .5];
b(n+2) = ye; % y=ye at t=te
b = b'; % make b into a column vector
u = A\b;
A
b'
u'
(u(2)-u(1))/h % initial velocity
% plot(-h/2:h:te+h/2, u, 'g'); % plot the coefficients
tv = 0:h/8:te; % supersample the parabolas
yv = [];
for t = tv
i = floor(t/h)+2;
if i==n+2
i = n+1;
end
x = t/h-i+1.5;
y = u(i-1)*.5*(x-.5)^2 + u(i)*(.75-x^2) + u(i+1)*.5*(x+.5)^2;
yv = [yv y];
end
% compute joints between elements
tk = (0:h:te)';
yk = .5*(u(1:n+1)+u(2:n+2));
hold off;
set(gca, 'FontSize', 16); % for tick marks
plot(tv,yv,'b', tk,yk,'bo', 'LineWidth',2);
xlabel('t', 'FontSize',20);
ylabel('y', 'FontSize',20);
axis([0 5 0 60]);
title('Galerkin Finite Element Method', 'FontSize',20);
Here is what the above code prints out.
>> galerkin(4)
A =
0.5000 0.5000 0 0 0 0
4.0000 -7.0000 2.0000 1.0000 0 0
1.0000 2.0000 -6.0000 2.0000 1.0000 0
0 1.0000 2.0000 -6.0000 2.0000 1.0000
0 0 1.0000 2.0000 -7.0000 4.0000
0 0 0 0 0.5000 0.5000
b =
0 -76.5625 -91.8750 -91.8750 -76.5625 40.0000
u =
-20.3125 20.3125 45.6250 55.6250 50.3125 29.6875
ans =
32.5000
Sometimes you can get the same accuracy with a smaller n,
using Galerkin instead of collocation.
So although it's more algebra and calculus to set up the Galerkin system,
and more computation to solve it, it is often worth the trouble to
use Galerkin.
We've discussed three methods: shooting, finite difference, and finite element. All of these methods transform boundary value problems into algebraic equation problems (a.k.a. root-finding). When the differential equation is linear, the system of equations is linear, for any of these methods. When the differential equation is nonlinear, the system of equations is, in general, nonlinear. Broyden's method, or other nonlinear system solver, could be used in the latter case.
Not discussed here: superposition method. Very useful for homogeneous linear ODE's.