An Introduction to Music Concepts
Roger B. Dannenberg
Introduction
This introduction is intended for computer science and engineering
students who are not trained musicians. My goal is to give a basic
introduction to concepts and give some formal terms and organization to
things that you probably already know about music. There is a strong
bias toward computation since our goal is to be generating music
automatically and computation is something you already know that we can
build from.
This document is hastily written to meet teaching deadlines. I want to
make this interesting and clear. Your feedback is most welcome.
Most of this presentation is about "Western tonal music" which implies
that the music probably has a beat, has familiar harmony, melody, etc.
To keep things simple, I will make a lot of generalizations and
describe music much more generally than I would like to. In particular,
you should be aware that music does not have to have beats, chords, and
other structures we will describe.
Rhythm
"Rhythm" refers to the musical organization of time. Most music has
"beats". If you can tap your foot to music, you will probably tap a
little faster than one tap per second. You will be tapping "beats."
Beats
The typical way to represent a beat in music notation is with a
"quarter note." (I'll tell you why it's a quarter note later.) The
symbol for a quarter note is:
It is also possible to draw the note
with the stem pointing down. It is not allowed to put the stem on the
other side of the note. It's on the right side when pointing up and the
left side when pointing down:
But one beat is not so interesting.
Beats establish a rhythm when the occur in sequence. We write a
sequence of beats by arranging them left-to-right on a line, like this:
If you clap your hands 4 times at a
steady pulse, you will be performing this little piece of music.
We might represent rhythms on the computer as an array of time points,
e.g. the little piece above could be represented by:
[0, 1, 2, 3]
Measures
Music is often described as hierarchical. There are beats, but you will
probably notice that not all beats are the same. Most popular music has
a higher level organization called a measure
that consists of 4 beats. Try listening to some rock music and see if
you can hear the 4-beat measures. You should feel something "big"
happening every 4 beats. (Hint: rock is usually pretty fast. For fast
rock, you'll be tapping about 2 or 3 beats per second. If you feel that
something "big" happens every 2 beats instead of 4 beats, don't worry
-- musical organization exists at many levels, so the 4-beat measure is
partly a matter of perception.)
To notate measures, we need some way of grouping our quarter note
beats. A vertical bar called a is used to separate measures. A working
musician will often call a measure a bar,
e.g. "give me a 2-bar intro." Here are 2 measures in notation:
We could represent this in code many ways. One is to used nested
arrays: an array of measures, each being an array of beat times:
[[0, 1, 2, 3], [4, 5, 6, 7]]
Alternatively, we could write a loop to generate measures and beats:
for m = 0 to 2
for b = 0 to 4
print "measure:", m, ", beat: ", b, " at time ", 4 * m + b
Duration
Music would be really boring if it only
had quarter notes. This would
mean that all events take place on the beat and last for one beat.
Music notation allows for different durations. As you might imagine, a
2-beat duration is a half
note, and a 4-beat duration is a whole
note. Going to shorter durations, half a quarter note is an eighth note, etc. Here's what they
look like:

Each measure still has four beats, but in some measures the durations
are shorter so more notes fit into those 4 beats. Notice that the last
measure has 4 sixteenth notes in the first beat and quarter notes in
the remaining three. I did this mainly to save space, but it makes the
point that you can combine durations any way you like as long as
durations add up to 4 beats.
Here's an array representation:
[[0],
[4, 6],
[8, 9, 10, 11],
[12, 12.5, 13, 13.5, 14, 14.5, 15, 15.5],
[16, 16.25, 16.5, 16.75, 17, 18, 19]]
Alternatively, we could write a loop to generate measures and beats:
durations = [4, 2, 1, 0.5, 0.25]
for m = 0 to 5
var b = 0
while b < 3.9999
print "measure:", m, ", beat: ", b, " at time ", 4 * m + b
b = b + durations[m]
This code generates 5 measures. In each measure, b is initialized to
zero, and b accumulates durations, and a different durations (looked up
in the array durations)
are used for each measure. Unlike the notation above, this actually
generates 16 sixteenth notes in the last measure to avoid coding the
special case.
Time Signature and Meter
Not all music is organized as 4 beats to the measure. There can be more
or less beats. Also, while it is typical for a quarter note to denote
one beat, sometimes different values get one beat. Mathematically,
there's no difference between a measure with 4 eighth notes played at
one eighth note per second and a measure with 4 quarter notes played at
one quarter note per second. To help make the notation clear, the number of beats per measure and the note value that gets one beat
are combined in something
called the time
signature. It's a bit like a type declaration in programming: it
constrains what goes into measures.
The time signature is the
notation for an abstract concept called meter. You can almost use "meter"
and "time signature" interchangeably, but if you are refering to the
music notation, use "time signature." Here is how we write the time
signature for 4 quarter notes:
In time signatures, the top number says how many beats to the measure,
and the bottom number says what rhythmic value gets one beat. E.g. a
"4" means a quarter note gets one beat, while a "2" means a half note
gets one beat. Here's a time signature for a waltz, which has 3
quarter-note beats per measure:
Another popular time signature is 6/8 time. If the music is slow, this
is performed with 6 beats per measure, typically in two groups of
three. At faster tempos, each group of three becomes one beat, so
really the signature should be 2/(8/3) meaning 2 beats per measure and
each beat corresponds to 3 eighth notes, but by convention, time
signatures are just two integers, so you are expected to know that 6/8
might be played "in two". (Note that 6 could also be divided into three
groups of two eighths, but in that case we can write 3/4 as shown
above.) Here are some measures of 6/8 meter:
Notice the eighths are "beamed" together. This is an alternative way to
notate an eighth note. The curved tails on the eighth note stems shown
earlier (see Section "Duration") are called flags, and the heavy bars shown
directly above are called beams.
Whether
drawn
with
flags
or
beams,
each
one
cuts
the
duration
in
half,
so
for
example,
you
could
draw
sixteenth
notes
with
double
beams.
The time signature 4/4 is also called "common time" (3/4 represented
the Holy Trinity and was used in church, so 4/4 was used in secular
music and therefore called "common"). Sometimes 4/4 is denoted with a
big "C". The signature 2/2 is very similar in that there are 2 half
notes = 4 quarter notes per measure, but we only divide the measure
into 2 beats. This is also called "cut time" and can be written with a
big "C" with a line through it:
Dots, Triplets, and Ties
So far, we've seen durations that are powers of two, but music allows
for other durations. The most general way to get new durations is
through addition. In music notation, this is achieved with a "tie": a
curved line that connects two adjacent notes. Ties can join any number
of notes. In the example below, notes have the durations of 1.5, 2.5,
1.75, 0.25, 0.5, and 1.5 beats:
In code, we could write the following, which computes the start time in
beats of each note, using addition corresponding to the ties in the
notation:
sixteenth = 1/16 // note: Serpent integer division returns a float
eighth = 1/8
quarter = 1/4
half = 1/2
t1 = 0
t2 = t1 + quarter + eighth
t3 = t2 + eighth + half
t4 = t3 + quarter + eighth + sixteenth
t5 = t4 + sixteenth
t6 = t5 + eighth
t7 = t6 + eighth + quarter
rhythm = [[t1, t2], [t3, t4, t5, t6]]
print "rhythm ends at time", t7
Since rhythms are based on integer relationships (subdividing into 2 or
3, ties are effectively adding small integers), 3 turns out to be a
very common duration. Music notation has a special way to introduce a
factor of 3 (well, actually the factor is 3/2): When a note is followed
by a dot, its duration is augmented by 50%; that is, the duration
becomes 3/2 of the original. Here is the first measure of the previous
notation example rewritten using a "dotted quarter note":
And here is the corresponding code. Notice the "quarter * 1.5"
expression to compute the duration of the dotted quarter.
eighth = 1/8
quarter = 1/4
half = 1/2
t1 = 0
t2 = t1 + quarter * 1.5
t3 = t2 + eighth + half
rhythm = [[t1, t2]]
print "rhythm ends at time", t3
If dots multiply by three, what about division by 3? This is also
common in music. Taking a beat and subdividing into 3 equal time units
creates a triplet, denoted by a little 3 above the note.
Usually triplets occur in groups, and often a curved line or square
bracket is used to show all the notes that are within the triplet.
Mathematically, the triplet notation multiplies the duration by 2/3.
While two eighth notes add up to a quarter note beat (0.5 + 0.5 = 1),
it takes 3 eighth note triplets to add up to a beat:
0.5 * 2/3 + 0.5 * 2/3 + 0.5 * 2/3 = 1
Here is what the notation looks like (this is in 4/4 time, but beats
are divided into triplets):
We could write some code to represent this rhythm:
et = 0.5 * 2/3 // duration of eighth note triplet
qt = 1 * 2/3 // duration of quarter note triplet
durations = [et, et, et, qt, et, et, et, et, et, qt]
sum = 0
rhythm = [] // compute the actual times of beats and put them here
for i = 0 to len(durations)
rhythm.append(sum)
sum = sum + durations[i] // keep running sum of durations
print rhythm, "next beat time is", sum
Rests
Silence is important! We have seen notation for musical events (notes),
but nothing to indicate that time passes without any events. A silent
duration in music is called a rest.
The
rest was as great an
invention as the number zero,
but that's another story. Just as there are symbols for note durations
in powers of two, there are symbols for rest durations in powers of
two. Dots and triplet markings apply to rests just like notes. Here are
the rests adding up to 3 measures of 4 beats:
We could write code do describe these rests, but usually, since
computer descriptions
contain timestamps for every event, there is no need for an explicit
representation of rests. Thus, in terms of our "array of measures"
representation, this is just three empty
measures: [[], [], []].
Summary
Rhythms are constructed from basic durations. There are symbols for
notes and rests
of different durations. The durations are powers of two: 4, 2, 1, 0.5,
0.25, etc., but
these may be added using ties, extended with dots, and scaled to get 3
in the time of 2 using triplet markings. In music notation, all time
must be accounted for, so if nothing
is happening, the silence is notated with a rest. The total durations
of rests and notes must add up to the duration of each measure. Measure
durations are "declared" using a time signature.
Pitch
Until now, we have shown notes all on one line, but you probably know
that music is usually drawn on multiple lines. The vertical dimension
of music notation denotes pitch,
which
relates
to
the
frequency
of
vibration
of
whatever
produces
the
musical
tone.
(Percussion
is
often
unpitched,
and
in
fact,
percussion
is
often
notated
on
a
single line as in the previous section on rhythm.)
Octaves
Before discussing notation of pitch, we need some pitch concepts. You
probably realize that there is a perception of height associated with
different pitches. High pitches are, well, higher, and low pitches are
lower. (I hope that makes sense. If not, try this: If a composer writes
about angels, you are going to hear high tinkly sounds with higher
frequencies, and when a composer writes about dark evil things, you are
going to hear low sounds with lower frequencies. There's something
about our perception that connects pitch height to physical height and
other connotations.)
But pitch is not just a range from low to high. There is a special
connection between pitches whose frequencies differ by a factor of
exactly 2. In some way, these pitches seem like two versions of the
same thing. They match even though one is much higher than the other.
This other quality is called chroma,
and
pitches
that
differ
in
frequency
by
a
factor
of
2
are
said
to
be
an
octave apart. (We should note
here that these pure mathematical notions don't always match up exactly
with human perception, but it's a good approximation. Still, it's my
duty to warn you that the story is deeper and richer than what you will
learn here.)
Octaves matter because our space of pitches seems to repeat itself
every factor of two in frequency, or every octave in pitch. For this
reason, we structure music pitch around octaves.
Division of the Octave
In Western tonal music (what we're talking about here), the octave is
divided into 12 equal intervals. If you look at the keys on a piano,
you will see a repeating pattern with 12 keys (7 white, 5 black):

This pattern repeats every octave. The thing that is equal about the
octave division is the frequency ratio
between adjacent pitches. For what it's worth the ratio is the 12th
root of 2 (but you could derive that, right?) This is called the equal-tempered scale because every
semitone is equal in terms of frequency ratio.
The sequence of pitches in this 12-note octave is called the chromatic scale. It's kind of
boring because every interval is the same, so there's no pattern and no
point of reference.
We usually represent pitches on the computer using integers for the
pitches of the chromatic scale. A particular note is called "Middle C"
(see the picture above), and Middle C gets the number 60. The next note
above Middle C is C-sharp (or C#), and has the number 61. We can
describe the chromatic scale as a sequence of integers:
chromatic_scale = []
for i = 60 to 73
chromatic_scale.append(i)
print "chromatic scale:", chromatic_scale
// this prints [60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72]
In addition to Middle C, every white key has a letter name. The letter
names for an octave are C, D, E, F, G, A, B. These pitch names repeat
in each octave. You would think the first pitch would be A, but it is
C. What difference does it make if the names are cyclic? As shown in
the figure above, Middle C is also called "C4." The "4" indicates the
octave, and from the numbering, you can see that the octave goes from C
to B: C4, D4, E4, F4, G4, A4, B4. Just above B4, we start a new octave
with C5.
Earlier, we said that there is a special similarity between pitches an
octave apart, so it should make sense that they all have similar names.
F2, F3, F4, F5, and F6 are all separated by exact octaves. Because they
share the same chroma, we can just say these are all different F's. A
set of pitches related by octaves is called a pitch class. There are of course 12
pitch classes.
Returning to our pitch numbers, notice that two pitch numbers with a
difference of 12 are an octave apart. We can number pitch classes too.
By convention, pitch classes are numbered from 0 to 12. The numerical
pitch class of any pitch P is just P modulo 12.
def pitch_class(p)
return p % 12
def same_pitch_class(p1, p2)
return pitch_class(p1) == pitch_class(p2)
Scales
A scale is a sequence of pitches, usually listed in increasing order,
starting at some initial pitch called the tonic. Usually,
a scale is the same in
every octave, so we all we need are the notes in one octave, or the
pitch classes, and where to start. Then we know all the scale notes.
Scales are usually composed from small intervals (usually just 1 or 2),
and the scales we will talk about
typically have 7 notes.
With 7 notes, you can construct scales where the intervals between
adjacent pitch classes are just 1 or 2. These scales with these 2
intervals (1 or 2, also called half steps and hole steps) are called diatonic
scales. The major scale,
is the most common one. The C major
scale is the major scale that starts on C and includes the white
notes of the piano: C, D, E, F, G, A, B. In contrast, there are pentatonic scales, with 5 notes,
constructed from intervals of 2 or 3. For example, C, D, F, G, A is a
pentatonic scale. Pentatonic scales are not diatonic scales.
We can describe a scale numerically as a starting pitch (or pitch
class) and a set of intervals above that pitch:
// C D E F G A B
c_major = [0, [0, 2, 4, 5, 7, 9, 11]]
Notice that all intervals are 2 (0 to 2, 2 to 4, etc.) except for the
interval from E (4) to F (5) and the interval from B (11) to C in the
next octave (12). If you look at the picture of the keyboard, you will
see that the only white notes not separated by black notes are in fact
E and F, and B and C.
Intervals
Pitch differences are called intervals. With numerical pitches, we can
just subtract to get a numerical representation of an interval:
// subtract the third scale interval (index=2) from the first (index=0):
major_third = c_major[1][2] - c_major[1][0]
But since music theorists started with pitch names and
diatonic scales, intervals are more complicated. To begin with,
intervals are based on counting scale steps from one pitch to another,
starting with 1. So the interval from C to E is counted like this: C
(1), D (2), E (3), and the answer is 3 (!). E is said to be a 3rd above
C because it is the 3rd note. It is also the third note in the C major
scale, so calling the interval from C to E a "third" does make some
sense. The second complication is that since
diatonic scale steps are not all the same size, counting scale steps
does not tell you everything. Here is how intervals, expressed as
numbers, are named:
- 0: unison
- 1: minor second, also a half step
- 2: major second, also a whole step
- 3: minor third
- 4: major third
- 5: perfect fourth
- 6: augmented fourth or diminished fifth
- 7: perfect fifth
- 8: minor sixth
- 9: major sixth
- 10: minor seventh
- 11: major seventh
The term "step" deserves some attention. Because intervals are based on
diatonic scale intervals, a "whole step" is actually 2 steps in the
chromatic scale (white keys and black
keys).
Therefore,
to
indicate
a
step
in
the
chromatic
scale
(numerically,
an
interval
of
1),
you
have
to
say "half step". It's
awkward. A "step" usually means "whole step", so don't think you can
call chromatic steps "steps" -- it will be confusing.
Where does the major scale (or any other) come from? Who decides where
to put the intervals of 1 and 2 (minor and major seconds)? It seems
arbitrary, but there is an interesting property of the major scale:
they come from a sequence of perfect fifths. Here's some code that,
strangely enough, computes c_major:
major = []
for i = 5 to 54 by 7
major.append(i % 12)
major.sort()
c_major = [0, major]
The final value of c_major will be [0, [0, 2, 4, 5, 7,
9, 11]], exactly as we wrote above. Look carefully at the code.
What it does is append 7 pitch classes separated by a fifth (modulo 12)
and sort them into ascending order. Why a perfect fifth? The perfect
fifth has a frequency ratio of 3:2. This is not quite as special as the
octave ratio 2:1, but it still has a strong perceptual salience. Maybe
it is not too surprising that common scales should have lots of fifths.
Scales can have the same set of intervals but start on different notes.
In our representation, the first number can be changed to shift the
scale to a new set of pitches. Here is a function that prints the pitch
classes of a scale:
// print the pitch classes of a scale
def print_scale(s) // s is in the form [base, [intervals...]]
var base = s[0]
var intervals = s[1]
for i in intervals
print (base + i) % 12,
print
For example, print_scale([4, [0, 2, 4, 5, 7, 9, 11]]) prints
the major scale that starts on 4 (i.e. E-major). The output is:
4, 6, 8, 9, 11, 1, 3
Using scales can make melodies more coherent. You can generate a random
pitch from a scale:
require "utils" // import the irandom() function
// return a random pitch class in scale s
def random_from_scale(s)
var base = s[0]
var intervals = s[1]
var r = intervals[irandom(len(intervals))]
return (r + base) % 12
Another possibility is to "adjust" a melody to use only pitches from a
given scale. Since a pitch can be at most a minor second (1) away from
a scale tone (assuming
diatonic scales), you can just test to see if a pitch is in the scale,
and if not, change it up or down by 1:
require "utils" // import the irandom() function
// irandom(n) returns a random number in [0...n-1], inclusive
// test if a pitch is in scale s
def in_scale_test(p, s)
var base = s[0]
var intervals = s[1]
p = (p + 120 - base) % 12 // (positive) interval from base to p
return (p in intervals) // tests for membership
def force_to_scale_tone(p, s)
if in_scale_test(p, s)
return p // already in the scale
// adjust up or down: 50% chance of either
if irandom(2) == 0
return p + 1
else
return p -1
// generate some random notes in a scale:
for i = 0 to 20
print force_to_scale_tone(irandom(24) + 12, c_major),
Although we have focused on the major scale, another common scale is
the minor scale. The
intervals of the minor scale are: [0, 2, 3, 5, 7, 8, 10], although
there are some variations on the minor scale with other intervals. One
version of minor (called melodic
minor) is different depending on whether you are going up or
down! Up is [0, 2, 3, 5, 7, 9, 11] and down is [12, 10, 8, 7, 5, 3, 2].
Pitch Notation
Music notation uses the vertical axis to indicate pitch. A set of 5
parallel horizontal lines, called a staff
is used as a grid for pitches. Notes are placed on the lines or between
the lines in the spaces. The pitches indicated by the lines and spaces
depend on the clef, a big
symbol at the left edge of each staff. The treble clef lines and spaces are
shown below. From bottom to top, the lines are EGBDF ("Every Good Boy
Deserves Favor") and the spaces are FACE. You can extend above and
below the staff by drawing ledger
lines to help the reader.
The bass clef lines and
spaces are shown below. The lines are GBDFA ("Good Boys Do Fine
Always"?) and ACEG ("All Cars/Cows Eat Grass/Gas", or for the climate
conscious, I suggest "All Cows Emit Gas").
The grand staff is a pair of
staves, one in treble clef, and one in bass clef, providing a pitch
range of about 3 octaves.
Accidentals and Key Signatures
Normally, the lines and spaces on a staff indicate the white notes of
the piano keyboard. The black notes are considered to be alterations of
the white notes. To alter a pitch to be one greater, we use a sharp sign, that looks like "#". To
alter a pitch to be one lower, we use a flat sign, that looks something
like "b". These are called accidentals.
Here are some notes with sharps and flats:
If you are playing on the scale of, say, C major, everything works out
well, but if you are playing in, say, C# major ([1, [0, 2, 4, 5, 7, 9, 11]]),
the pitches of the scale are C#, D#, E#, F#, G#, A#, B#. That's a lot
of accidentals! Rather than write a sharp sign in front of every note,
we put the sharps over on the left side of each staff to efffectively
relable the staff lines and spaces to denote different pitches. This is
called a key signature.
Instead of saying "I'm playing on the scale of C# major," we say "I'm
playing in the key of C# major." Here is what music in the key of C#
major looks like:
Even though the notes do not have individual accidentals, each note is
played a half-step higher because each is affected by the key signature
on the left. The details of how to lay out key signatures is
interesting and relates
to the those perfect fifth intervals, but we will stop here with
pitches so we can move on to harmony.
One thing we should add is that the notions of key and scale are almost identical. The
difference is just that "key" is used when talking about the set of
pitches and their harmonic implications ("this piece is in the key of C
minor"), whereas "scale" is a specific sequence of pitches ("this
melody is derived from the C minor scale").
Transposition
When every note of a melody is shifted up or down by some fixed number
of half-steps (semitones), the result is recognizable as the same
melody. It may sound higher or lower, but it is not a new melody.
Shifting pitches is called transposition.
A transposition is defined by an interval,
e.g.
we
can
transpose
up
by
a
perfect
fifth
or
down
by
a
whole
step.
Numerically,
tranposition is just integer addition. The following code
transposes a pitch set or sequence (an array of integers):
melody = [71, 71, 72, 74, 74, 72, 71, 69, 67, 67, 69, 71, 71, 69, 69]
def pitch_transpose(pitch, interval)
pitch + interval
def melody_transpose(melody, interval)
var new_melody = melody.copy() // make new result array same length
for p at i in melody
new_melody[i] = pitch_transpose(p, interval)
print "melody up a fifth is:", melody_transpose(melody, 7)
Summary
Pitch has structure. Pitches separated by octaves are related (they
share the same pitch class). The octave is divided into 12 equal
intervals, but most scales use only a subset of these. For example, the
C major scale uses only the white keys on the piano. Diatonic scales
are built from intervals of 1 or 2 (minor seconds and major seconds).
Pitch classes are labeled with letters, and pitches are labeled with
the pitch class and an octave number. The "black keys" are named using
accidentals to alter the "white key pitches" up or down. Pitches are
indicated by the lines and spaces of the staff, and different clefs are
typically used to map a convenient range of pitches to the lines and
spaces.
Harmony
Harmony "happens" when multiple pitches are played at once. It is not
known exactly what happens in your brain or why, but some pitch
combinations sound "harmonious" or consonant
while others clash and sound dissonant.
You should be careful about confusing consonant with "good" or
dissonant with "bad." Even in popular music, dissonance at some level
is essential to create an expectation of or desire for resolution to
consonance.
Intervals
We already discussed intervals. An interval
defines a two-note chord. Some intervals are more consonant and others
are more dissonant. Generally, intervals that correspond to frequency
ratios that are simple integer fractions are the most consonant. A
special case is the octave, with a frequency ratio of 2:1, which is so
consonant it is sometimes hard to hear as anything other than two
instruments playing the same note, and if it is really in tune or
electronically generated, you might only hear one pitch. You cannot
easily tell what intervals have simple frequency ratios just by looking
at the difference in semitones. For example, the perfect fifth (7
semitones) is irrational in the equal-tempered scale (the 12th root of
2 to the 7th power), but the fifth is very close to the ratio 3:2.
Triads
A chord with three pitches is called a triad. There are many triads, but
only a few really important ones. The major
triad or just "major chord," consists of a major third and a
perfect fifth as measured from the lowest pitch. Numerically, this is
[0, 4, 7]. You can also look at this in terms of successive intervals:
c_major
4 - 0 = 4 (a major third), and 7 - 4 = 3 (a minor third). So a major
chord is a minor third on top of a major third.
Notic the sharps. The first is necessary because the interval from A to
C is 3 half-steps or a minor third, so we have to use a C# instead of
C. Similarly, in the last chord, both the D and F need to be sharped to
get the right intervals.
Another way to think about chords is through their relationship to
scales. Notice that the C Major triad is the first, third, and fifth
notes of the C Major scale. You can build most common chords by taking
3 to 5 alternating notes of diatonic scales!
Another important chord is the minor
triad or "minor chord." The minor chord has a minor third and a
perfect fifth: [0, 3, 7] (you will find these intervals in the minor
scale, discussed earlier). You could also say this is a major third
(from 3 to 7) on top of a minor third (from 0 to 3). Here are some
notated minor thirds:
Compared to the major triads, you can see that each middle note is
lowered by one half step, either by adding a flat (in the first
measure), or by removing a sharp (in the second measure).
Chord Types
There are many chord types, and basic chords like the major and minor
triads can be extended by adding new pitches. For example, a
C-major-ninth chord has a minor seventh and a major ninth (equivalent
to a major second) added to the major triad. Here are the intervals for
more common chords:
Major Triad (Maj)
|
[0,
4,
7]
|
Minor Triad (min)
|
[0, 3, 7]
|
Diminished Triad (dim)
|
[0, 3, 6]
|
Augmented Triad (aug)
|
[0, 4, 8]
|
Major Seventh (Maj7)
|
[0, 4, 7, 11]
|
Minor Seventh (min7)
|
[0, 3, 7, 10]
|
Dominant Seventh (7)
|
[0, 4, 7, 10]
|
Diminished Seventh (dim7)
|
[0, 3, 6, 10]
|
Diminished Sixth (dim6)
|
[0, 3, 6, 9]
|
Roots
The groups of chords shown above are all major or minor, but obviously
they are different. While the intervals are the same, the actual
pitches are different. The triads are different transpositions of the same chord.
We describe the transposition by using the name of the bottom note of
the triad. This is called the root.
So the first major chord shown above is "C major" and the last minor
chord shown is "B minor." We say that the root of the C major triad is
C.
Just as with scales, which we represented as a starting pitch class and
a set of intervals, we can represent triads (or any chord) as a root
and a set of intervals:
c_maj = [0, [0, 4, 7]]
d_maj = [2, [0, 4, 7]]
f_min = [5, [0, 3, 7]]
Of course, there is nothing "correct" or magical about these
representations. You should think about representations that are best
for your particular work. You can change representations:
# "root_interval" notation means [root, [...set of intervals above the root...]]
# "pitch_set" notation means [... set of pitch numbers ...]
#
# convert to pitch_set:
def root_interval_2_pitch_set(ri)
var root = ri[0]
var intervals = ri[1]
var ps = []
for interval in intervals
ps.append(root + interval)
return ps
# convert to root_interval:
# (to make this problem simpler, we will explicitly give the root pitch)
def pitch_set_2_root_interval(ps, root)
var ri = []
for p in ps
ri.append((1200 + p - root) % 12)
# sort the intervals in increasing order
# (In principle, we should remove duplicates as well.)
return [root, ri.sort()]
The pitch_set_2_root_interval function
illustrates a problem which is determining the root of a chord. You
might assume the root is the bottom note, but things are not so simple.
Inversions
Because of the special quality of octaves, you can shift any note in a
chord by an octave, and the result is the same chord. E.g. [60, 64, 67]
is a C-major triad starting on middle C. [72, 64, 67] is also a C-major
chord. You could conceivably say this is some other chord with a root
of E (64):
pitch_set_2_root_interval([72, 64, 67], 64) ==> [64, [0, 3, 8]]
but the problem is this still sounds like C-major. There are actually 3
ways to represent the intervals in a major chord. We've seen [0, 4, 7] and we just
encountered [0, 3, 8].
The
last
is
[0, 5, 9].
These are simply "rotations" or what musicians call inversions of the major chord.

As a consequence, intervals are not the
whole story. You need to know the root of a chord and put the root on
the bottom to identify the chord type. Unfortunately, things can be a
bit ambiguous, especially when there are more then three notes in the
chord. For example, a C-sixth chord is a C-major triad with an added
major sixth interval (in pitch_set format, we could write [60, 64, 67, 69]) and an
A-minor-seventh chord is an A-minor triad with an added minor seventh
interval ([69, 72, 76, 79]).
Subtracting
12
from
the
last
three
pitches,
we
get
[69,
60, 64, 67], which is just
a permutation of the C-sixth chord.
Voicing
The fact that chord can exist in different inversions and that chord
tones can appear in different octaves gives great flexibility to the
composer. The arrangement of pitches in a chord is called the voicing. Chords are often voiced to
so that there are only small pitch changes from the previous chord.
Small pitch changes give a sense of continuity and melody.
Another aspect of voicing is the spread between tones and doublings, meaning repetition of
notes at octaves. Closed voicings
minimize the distance between chord tones. The music notation just
above shows closed voicing for the C-major triad. Open voicings have greater distance
between chord tones. Some open voicings are shown below, and in the
last chord, the root (C) and fifth (G) appear in two different octaves,
an example of doubling. Here, chords are notated on a grand staff
(discussed earlier) which is typically used for piano music and gives a
wider pitch range than a single 5-line staff.
Notice the top note of the first chord: this is on the second line
above the bass clef and represents E, which you can determine by
counting spaces and lines up from the top line of the bass clef (which
is A). This E could also be notated as the bottom line of the treble
clef. Generally, the treble clef is played by the right hand and the
bass by the left, but otherwise the note is the same. It is also good
to be aware that notes below the treble clef are not necessarily lower
in pitch, as in this case.
The purpose of open voicings is to get a wider pitch spread. It's a
different quality of sound and usually preferable if you want a piano
accompaniment to sound big and full.
Alterations
In popular music, it is common for performers and arrangers to alter
chord voicings and even change chords. This can be done while still
preserving the melody and the "function" of the harmony. Aside from
octave doublings we saw in the discussion of voicing (above), the
following alterations are usually reasonable, and many other
alterations and substitutions are possible:
Major [0, 4, 7]
|
Add major 7th [0, 4, 7, 11]
Add major 6th [0, 4, 7, 9]
Add major 7th and 9th [0, 4, 7, 11, 14]
|
Minor [0, 3, 7]
|
Add minor 7th [0, 4, 7, 10]
Add major 6th [0, 4, 7, 9]
Add minor 7th and major 9th [0, 4, 7, 10, 14]
|
Dominant 7th [0, 4, 7, 10]
|
Add major 9th [0, 4, 7, 10, 14]
Add "flat 9" [0, 4, 7, 10, 13]
|
Summary
Chords are combinations of pitches. Chords are usually considered
equivalent if they have the same set of pitch classes. Finding the root
of a chord is non-trivial, but finding a set of actual pitches, given a
root and the intervals of the chord (such as in the table above), is
easy. Choosing octaves and doublings for each pitch class in a chord is
called voicing. Chords can
also be altered to change the quality of the harmony.
Form
Musical form is a general term for structures above the level of
melody, harmony, and rhythm. There is not a general theory of form, but
many examples of how music is organized into larger structures.
Motives, Phrases, Melody, and Chord Sequences
We combine sequences of pitches, usually played in a specific rhythm to
form melody. Often, melodies
have substructure. A phrase is
a
kind
of
musical "statement" that usually feels incomplete. The end of
a phrase is where you might take a breath if you are singing a song,
but phrases that do not complete the melody usually end in a way that
suggests more is to follow.
How do you "suggest more is to follow"? One clue is that pitches that
end on the tonic (the initial note of the scale) sound more "final"
than others. A melody will generally sound incomplete unless it ends on
the tonic.
Sometimes, melodies include short
distinctive phrases or sub-phrases called motives (or sometimes motifs). The most famous example is
the four-note motive at the beginning of Beethoven's Fifth Symphony,
which is used as a rhythmic and melodic building-block throughout the
entire symphony:
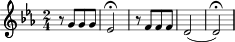 Source: Wikipedia
(image is public domain)
Source: Wikipedia
(image is public domain)
Chord sequences are the foundation of harmonic structure. Just as pitch
sequences sound complete and come to rest on the tonic of a scale,
chord sequences tend to end on the tonic
chord, the triad consisting of the tonic,
third, and fifth notes of the scale (a major triad if in a major
scale, and a minor triad if in a minor scale).
There are many common chord progressions. Most songs are filled with
"conventional" chord transitions but often have an unusual chord
transition or two. As with melody, rhythm, and harmony, if all the
elements are completely expected and most likely, there are no
surprises and the music can be very boring. On the other hand, if
everything is a surprise, the music can sound completely incoherent,
and again boring.
An aside: Modern composers often struggle to get away from tonal
harmony and the common musical stuctures discussed here. This often
sounds random to ears unaccustomed to this approach. Interestingly, if
you avoid tonal music, your choices are anything but random, so even
atonal music has a lot of predictability which you learn to hear with
experience.
Common chord progressions are usually related to the interval of the
fifth. In particular, a descending
fifth is heard as a kind of resolution. E.g. a very final sounding
final chord transition, or cadence,
is
G
major
to C major. Almost any movement up or down by a fifth within the scale is common.
Let's discuss that phrase "within the
scale" in some detail. Although there are exceptions within
almost every popular song, for the most part song melodies stay within
a scale, and chords that accompany the melody also use pitches from the
scale. Recall that the interval of a fifth is 7 semitones. If we shift
(transpose) all notes of a chord up by exactly 7 semitones, this is
called a chromatic transposition. If we shift within the scale, we
would shift up by 4 scale tones. This is called a tonal transposition. Tonal
transposition takes place within a designated scale or key.
c_major = [0, [0, 2, 4, 5, 7, 9, 11]] // C Major scale
c_minor = [0, [0, 2, 3, 5, 7, 8, 10]] // C minor scale
major_mode = c_major[1] // intervals of the major scale
minor_mode = c_minor[1] // intervals of the (natural) minor scale
# "root_interval" notation means [root, [...set of intervals above the root...]]
# "pitch_set" notation means [... set of pitch numbers ...]
#
# convert to pitch_set:
def root_interval_2_pitch_set(ri)
var root = ri[0]
var intervals = ri[1]
var ps = []
for interval in intervals
ps.append(root + interval)
return ps
# convert to root_interval:
# (to make this problem simpler, we will explicitly give the root pitch)
def pitch_set_2_root_interval(ps, root)
var ri = []
for p in ps
ri.append((1200 + p - root) % 12)
# sort the intervals in increasing order
# (In principle, we should remove duplicates as well.)
return [root, ri.sort()]
# compute the tonal tranposition of p by interval within scale
# interval is 1=unison, 2=second, 3=third, etc.
def pitch_tonal_transpose(p, interval, scale)
var pc = p % 12 // pitch class of p
// how many semitones is pc above the root of the scale?:
var steps_from_root = (p + 1200 - scale[0]) % 12
// what scale step is this (zero-based offset):
var scale_step = scale[1].index(steps_from_root)
if scale_step == -1 // -1 means "not found in array"
return "pitch is not in the scale"
// compute the scale index after transposition
var transposed = (scale_step + interval - 1)
// shift tranposed (an index) to be within array of intervals
// keep track of octaves by adding/subtracting to octave
var octave = 0
while transposed < 0
transposed = transposed + len(scale[1])
octave = octave - 12
while transposed >= len(scale[1])
transposed = transposed - len(scale[1])
octave = octave + 12
// add the transposition in semitones to p:
return p + octave + scale[1][transposed] - steps_from_root
def chord_tonal_transpose(chord, interval, scale)
// first transpose the root
var new_root = pitch_tonal_transpose(chord[0], interval, scale)
// compute and transpose each pitch:
var pitches = root_interval_2_pitch_set(chord)
for p at i in pitches
pitches[i] = pitch_tonal_transpose(p, interval, scale)
return pitch_set_2_root_interval(pitches, new_root)
// example: print all tonal transpositions of C-major (in key of C)
c_major_triad = [60, [0, 4, 7]]
for i = 0 to 7
var triad = chord_tonal_transpose(c_major_triad, i + 1, c_major)
print triad, "=", root_interval_2_pitch_set(triad)
// OUTPUT LOOKS LIKE THIS:
[60, [0, 4, 7]] = [60, 64, 67]
[62, [0, 3, 7]] = [62, 65, 69]
[64, [0, 3, 7]] = [64, 67, 71]
[65, [0, 4, 7]] = [65, 69, 72]
[67, [0, 4, 7]] = [67, 71, 74]
[69, [0, 3, 7]] = [69, 72, 76]
[71, [0, 3, 6]] = [71, 74, 77]
Notice that with tonal transposition, intervals measured in semitones
are not preserved. For example, in the second line of output, we see
that when we transpose a C Major triad up one step, the result is a D
minor triad.
The length of this code may seen daunting. Most of the code is dealing
with translations between representations as semitones, scale steps,
relative intervals, and absolute pitches. In this case, it would be
easier to work with scale steps (7 steps to the octave). Then tonal
transposition would be simple addition.
For computer generated music, it might make more sense to store chords
in a table, similar to the output shown above. Then, the chords can be
transposed chromatically to
any desired key.
Typical chord progressions start on the tonic, move away from the
tonic, and return to the tonic. The return often involve descending
tonally by fifths. Another principle of chord progressions is that
transitions seem to make more sense when the two chords share at least
one pitch. Notice that since major and minor chords contain the
interval of the fifth, that a transposition up or down by a fifth will
always result in a common tone. Wikipedia's article on "Chord
progression" gives a number of examples.
Repeats
Aside from continuity, the
idea that small intervals in melody and common tones in chords lead to
smooth transitions, one of the strongest ways to create structure in
music is repetition. Several completely random elements in sequence
become identifiable as a unit when they are repeated. Repetition also
creates tension. If you repeat something, the listener knows that
change is inevitable. Repetition creates the anticipation of change,
and this tension is resolved when the change takes place (although if
the music changes to something dissonant or jarring, the release of
tension from the repetition may be replaced by new tension.)
In computer generated music, random algorithms are often used to
generate sequences. If these sequences lack repetition at the level of
phrases or melodies, then they will miss out on a structural element
that is very common in most music. One of the tricks of all composers
is repetition with variation. A literal repetition can be boring, so
often composers make small changes such as voicing chords differently,
adding another accompanient voice, changing the rhythm, etc., while
repeating other aspects of the music.
Structure Notation
A common way to notate structure is to denote different sections of
music with different letters, e.g. AAA means the phrase or section
denoted by "A" is played 3 times.
Rondo
The rondo form is ABACADA,
and so on. In other words, a theme "A" is followed by new, contrasting
material. Each time, the music returns to the "A" theme.
Song Form
The song form, also called
the 32-bar form, or AABA form became popular only in
the 20th Century, but it is very common in pop, rock, and jazz tunes.
The AABA form consists of 8 measures (A) called the verse that repeats, followed by an
8-measure contrasting B section called the bridge, followed by one more A
section. The A section usually begins and ends on the tonic chord while
the bridge often ends on a dominant seventh chord (which resolved to
the beginning of the final A section).
Summary
Form is the general term for higher-level structures in music. Form is
often notated with strings. The most important generator of structure
and tension in music is repetition. One can almost say that until music
either repeats or fails to repeat, there is no form. Common forms
include simple repetition, rondo, and song form.
Closing Words
This introduction was written for "Computer Music Systems and
Information Processing," a computer science course at Carnegie Mellon
University taught by the author. If you have questions, find errors, or
have any suggestions about how to present these concepts more clearly
or with better motivation, please let me know (rbd at cs.cmu.edu).










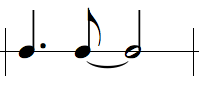
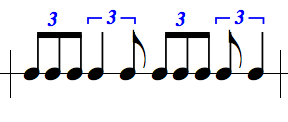






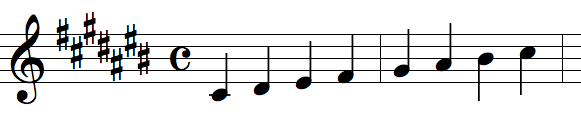



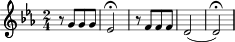 Source: Wikipedia
(image is public domain)
Source: Wikipedia
(image is public domain)