
Abstract
The beauty of many algebraic problems (solving system of equations, proving inequality, ...) comes from the symmetric / cyclic properties of its variables. These properties also exist in a class of number theory problems, but require a different approach to utilize, as the variables in this context are often natural numbers or integers, instead of real numbers. In this article we mention two directions that can be taken into account to solve a variety of cyclic problems. The reader is encouraged to gain familiarity with the technique of Vieta jumping and the concept of p-adic order νp(n), both of which are employed throughout this writing.
This method is often used in divisibility problems with cyclic conditions

If gcd(a,b) = 1, we can construct two functions g : ℤ → ℤ and h : ℤ2 → ℤ such that:
It then follows that
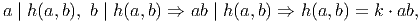 | (1) |
for some k ∈ ℤ. (1) is a two-variable equation in terms of a and b. If deg h = 1 we can use inequalities to restrict the domain of a and b to a finite subset of ℤ. If deg h = 2 we can use Vieta jumping to solve (1).
Without gcd(a,b) = 1, we still have ab∣f(a)f(b). We can then expand the RHS and remove all multiples of ab, essentially ending up with an equation similar to (1).
Solution. Let a = p - 1, b = q - 1 then a ≥ b ≥ 1 and
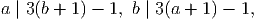
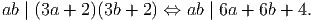
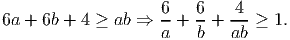


| b | Condition for a | Values of a |
| 1 | a∣6a + 6 + 4 | {1, 2, 10} |
| 2 | 2a∣6a + 12 + 4 | {2, 4} |
| 4 | 4a∣6a + 24 + 4 | {6, 10} |
| 6 | 6a∣6a + 36 + 4 | ∅ |
| 10 | 10a∣6a + 60 + 4 | {16} |
| 12 | 12a∣6a + 72 + 4 | ∅ |
Hence all possible values of (p,q) are (2, 2); (3, 3); (5, 3); (7, 5); (17, 11). __
Example 2. Find the number of tuples (a,b,c) where a < b < c are positive and pairwise coprime integers satisfying

Solution. As a∣bc - 31 and a∣a(b + c) we have
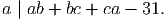
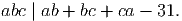 | (2) |
Now consider the following cases:

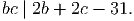
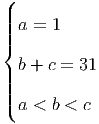
Hence 1 < b < c < 31. Combining with b∣c - 31 and c∣b - 31, we get

To sum up, the case a = 1 yields 16 possible values of (b,c).
Hence we conclude that there are in total 17 possible tuples (a,b,c). __
Remark 1. In the previous two examples, we try to arrive at a condition of the form

Solution. From


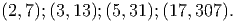
| p∣(q2 + q + 1) + (p2 + p), and | |||
| q∣(p2 + p + 1) + (q2 + q), |
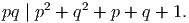
 | (3) |
Rewrite (3) as
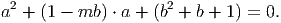
| a0 + a′ = mb0 - 1, | (4) | |
| a0a′ = b02 + b 0 + 1. | (5) |

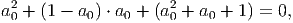
 | (6) |
As we proved earlier, if (a0,b0) is a solution then so is (5a0 - b0 - 1,a0). Hence from one solution (1, 1) we get (3, 1), and then (13, 3), ... We can in fact prove that all solutions of (6) are (ai,bi) = (xi+1,xi) where xis come from the sequence

In conclusion, all possible values of p and q are (2, 7); (3, 13); (5, 31); (13, 61); (17, 307). __
If the variables are symmetric, we can sort them in ascending or descending order. If the variables are cyclic, we can point out one variable with some maximum / minimum property.
Example 4. Consider arbitrary positive numbers a,b,c. Denote (a,b) and [a,b] as the greatest common divisors and lowest common multiples of a and b respectively. Prove that
![(a,b) ⋅-(b,c)-⋅ (c,a) [a,b] ⋅ [b,c] ⋅ [c,a]
(a,b,c)2 = [a,b,c]2 .](cyclic-number-theory27x.png)
Solution. Let L and R denote the LHS and RHS of the equality repspectively. Consider an arbitrary prime p. If p ∤ [a,b,c] then it’s obvious that νp(L) = νp(R) = 0. On the other hand, if p∣[a,b,c] then either p∣a or p∣b or p∣c. Let x = νp(a), y = νp(b), z = νp(c). As a,b,c are symmetric, WLOG assume x ≥ y ≥ z, then
| νp(L) = y + z + z - 2z = y | ||
| νp(R) = x + y + x - 2x = y |
Solution. WLOG assume p ≤ q. Consider the following cases:
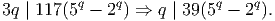
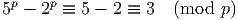
 | (7) |
Consider the following equivalences in mod p:

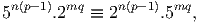
In conclusion, all possible values of (p,q) are (3, 3); (3, 13); (13, 3). __
Solution. First note that for any x ∈ ℤ, gcd(x - 1,x + 1) = gcd(2,x + 1) ≤ 2.
WLOG assume p ≥ q. If p = q then p2∣2p+1 ⇒ p = q = 2. If p > q:
 | (8) |
Let a be the smallest positive integer satisfying 2a ≡ 1 (mod q) (i.e., a is the order of 2 in ℤq). By the property of order,

| 2(p - q) | = 2k+1 ⋅ m, | ||
| q - 1 | = 2l ⋅ n |
| 2(p - q)s | = am | ||
| (q - 1)m | = (p - q) ⋅ n ⋅ 2l-k-1. |
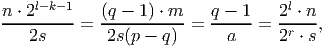
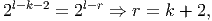
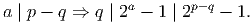 | (9) |
From (8) and (9) we see that q∣(2p-q - 1, 2p-q + 1). On the other hand, gcd(2p-q - 1, 2p-q + 1) ≤ 2 as remarked earlier, so it follows that q = 2. However, this is false since we are assuming q > 2.
In conclusion, all values of (p,q) are (2, 2); (2; 3), (3; 2).
Example 7. Consider positive integers x,y,z where (xy +1)(yz +1)(zx+1) is a square. Prove that each of xy + 1,yz + 1 and zx + 1 is also a square.
Solution. Let S = {(x,y,z)∣(xy + 1)(yz + 1)(zx + 1) is square}. Consider the tuple
(x,y,z) ∈ S where x + y + z is smallest. WLOG assume z = max{x,y,z}.
Let t be a root of the equation.

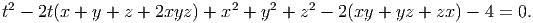 | (10) |
Note that (10) is equivalent to the following three equations:
| (x + y - z - t)2 = 4(xy + 1)(zt + 1) | (11) | |
| (x + z - y - t)2 = 4(xz + 1)(yt + 1) | (12) | |
| (x + t - y - z)2 = 4(xt + 1)(yz + 1) | (13) |
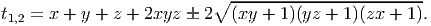
| [(x + y + z - t)(x + z - y - t)(x + t - y - z)]2 | |||
| = | [8(xy + 1)(yz + 1)(zx + 1)]2 ⋅ [(xt + 1)(yt + 1)(zt + 1)], |


| t1t2 | = x2 + y2 + z2 - 2(xy + yz + zx) - 4 | ||
| ≤ z2 - x(2z - x) - y(2z - y) | |||
| < z2, |
In conclusion, each of xy + 1,yz + 1 and zx + 1 is a square. __
Solution. WLOG assume a ≤ b ≤ c. As 91 is not a square, we have a,b,c≠0.
If a ≥ 0 and b,c ≥ 0 so a2 - bc < 0 < 91, which is false. Hence a < 0.
Also observe that if (a,b,c) satisfies the system of equations then so does (-a,-b,-c).
Hence we only need to consider the tuples (a,b,c) where c > 0.
Now if b = c then
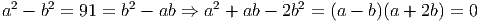
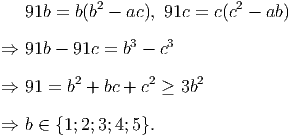
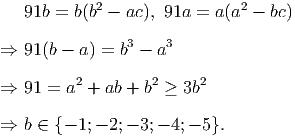
In conclusion, all possible values of (a,b,c) are (-10, 1, 9), (10,-1,-9), (-11, 5, 6), (11,-5,-6), (-9,-1, 10), (9, 1,-10), (-6,-5, 11), and their permutations. __