Reed-Solomon Codes
An introduction to Reed-Solomon codes: principles, architecture and implementation
1. Introduction
Reed-Solomon codes are block-based error correcting codes with a wide range of applications in digital communications and storage. Reed-Solomon codes are used to correct errors in many systems including:
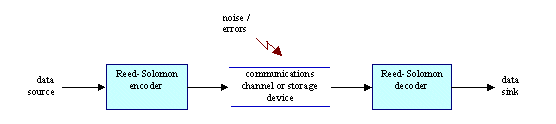
A typical system is shown here:

The Reed-Solomon encoder takes a block of digital data and adds extra "redundant" bits. Errors occur during transmission or storage for a number of reasons (for example noise or interference, scratches on a CD, etc). The Reed-Solomon decoder processes each block and attempts to correct errors and recover the original data. The number and type of errors that can be corrected depends on the characteristics of the Reed-Solomon code.
2. Properties of Reed-Solomon codes
Reed Solomon codes are a subset of BCH codes and are linear block codes. A Reed-Solomon code is specified as RS(n,k) with s-bit symbols.
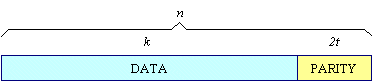
This means that the encoder takes k data symbols of s bits each and adds parity symbols to make an n symbol codeword. There are n-k parity symbols of s bits each. A Reed-Solomon decoder can correct up to t symbols that contain errors in a codeword, where 2t = n-k.
The following diagram shows a typical Reed-Solomon codeword (this is known as a Systematic code because the data is left unchanged and the parity symbols are appended):
Example: A popular Reed-Solomon code is RS(255,223) with 8-bit symbols. Each codeword contains 255 code word bytes, of which 223 bytes are data and 32 bytes are parity. For this code:
n = 255, k = 223, s = 8
2t = 32, t = 16
The decoder can correct any 16 symbol errors in the code word: i.e. errors in up to 16 bytes anywhere in the codeword can be automatically corrected.
Given a symbol size s, the maximum codeword length (n) for a Reed-Solomon code is n = 2s – 1
For example, the maximum length of a code with 8-bit symbols (s=8) is 255 bytes.
Reed-Solomon codes may be shortened by (conceptually) making a number of data symbols zero at the encoder, not transmitting them, and then re-inserting them at the decoder.
Example: The (255,223) code described above can be shortened to (200,168). The encoder takes a block of 168 data bytes, (conceptually) adds 55 zero bytes, creates a (255,223) codeword and transmits only the 168 data bytes and 32 parity bytes.
The amount of processing "power" required to encode and decode Reed-Solomon codes is related to the number of parity symbols per codeword. A large value of t means that a large number of errors can be corrected but requires more computational power than a small value of t.
Symbol Errors
One symbol error occurs when 1 bit in a symbol is wrong or when all the bits in a symbol are wrong.
Example: RS(255,223) can correct 16 symbol errors. In the worst case, 16 bit errors may occur, each in a separate symbol (byte) so that the decoder corrects 16 bit errors. In the best case, 16 complete byte errors occur so that the decoder corrects 16 x 8 bit errors.
Reed-Solomon codes are particularly well suited to correcting burst errors (where a series of bits in the codeword are received in error).
Decoding
Reed-Solomon algebraic decoding procedures can correct errors and erasures. An erasure occurs when the position of an erred symbol is known. A decoder can correct up to t errors or up to 2t erasures. Erasure information can often be supplied by the demodulator in a digital communication system, i.e. the demodulator "flags" received symbols that are likely to contain errors.
When a codeword is decoded, there are three possible outcomes:
1. If 2s + r < 2t (s errors, r erasures) then the original transmitted code word will always be recovered,
OTHERWISE
2. The decoder will detect that it cannot recover the original code word and indicate this fact.
OR
3. The decoder will mis-decode and recover an incorrect code word without any indication.
The probability of each of the three possibilities depends on the particular Reed-Solomon code and on the number and distribution of errors.
Coding Gain
The advantage of using Reed-Solomon codes is that the probability of an error remaining in the decoded data is (usually) much lower than the probability of an error if Reed-Solomon is not used. This is often described as coding gain.
Example: A digital communication system is designed to operate at a Bit Error Ratio (BER) of 10-9, i.e. no more than 1 in 109 bits are received in error. This can be achieved by boosting the power of the transmitter or by adding Reed-Solomon (or another type of Forward Error Correction). Reed-Solomon allows the system to achieve this target BER with a lower transmitter output power. The power "saving" given by Reed-Solomon (in decibels) is the coding gain.
3. Architectures for encoding and decoding Reed-Solomon codes
Reed-Solomon encoding and decoding can be carried out in software or in special-purpose hardware.
Finite (Galois) Field Arithmetic
Reed-Solomon codes are based on a specialist area of mathematics known as Galois fields or finite fields. A finite field has the property that arithmetic operations (+,-,x,/ etc.) on field elements always have a result in the field. A Reed-Solomon encoder or decoder needs to carry out these arithmetic operations. These operations require special hardware or software functions to implement.
Generator Polynomial
A Reed-Solomon codeword is generated using a special polynomial. All valid codewords are exactly divisible by the generator polynomial. The general form of the generator polynomial is:
and the codeword is constructed using:
c(x) = g(x).i(x)
where g(x) is the generator polynomial, i(x) is the information block, c(x) is a valid codeword and a is referred to as a primitive element of the field.
Example: Generator for RS(255,249)
3.1 Encoder architecture
The 2t parity symbols in a systematic Reed-Solomon codeword are given by:
![]()
The following diagram shows an architecture for a systematic RS(255,249) encoder:

Each of the 6 registers holds a symbol (8 bits). The arithmetic operators carry out finite field addition or multiplication on a complete symbol.
3.2 Decoder architecture
A general architecture for decoding Reed-Solomon codes is shown in the following diagram.

Key
| r(x) | Received codeword |
| Si | Syndromes |
| L(x) | Error locator polynomial |
| Xi | Error locations |
| Yi | Error magnitudes |
| c(x) | Recovered code word |
| v | Number of errors |
The received codeword r(x) is the original (transmitted) codeword c(x) plus errors:
r(x) = c(x) + e(x)
A Reed-Solomon decoder attempts to identify the position and magnitude of up to t errors (or 2t erasures) and to correct the errors or erasures.
Syndrome Calculation
This is a similar calculation to parity calculation. A Reed-Solomon codeword has 2t syndromes that depend only on errors (not on the transmitted code word). The syndromes can be calculated by substituting the 2t roots of the generator polynomial g(x) into r(x).
Finding the Symbol Error Locations
This involves solving simultaneous equations with t unknowns. Several fast algorithms are available to do this. These algorithms take advantage of the special matrix structure of Reed-Solomon codes and greatly reduce the computational effort required. In general two steps are involved:
Find an error locator polynomial
This can be done using the Berlekamp-Massey algorithm or Euclid’s algorithm. Euclid’s algorithm tends to be more widely used in practice because it is easier to implement: however, the Berlekamp-Massey algorithm tends to lead to more efficient hardware and software implementations.
Find the roots of this polynomial
This is done using the Chien search algorithm.
Finding the Symbol Error Values
Again, this involves solving simultaneous equations with t unknowns. A widely-used fast algorithm is the Forney algorithm.
4. Implementation of Reed-Solomon encoders and decoders
Hardware Implementation
A number of commercial hardware implementations exist. Many existing systems use "off-the-shelf" integrated circuits that encode and decode Reed-Solomon codes. These ICs tend to support a certain amount of programmability (for example, RS(255,k) where t = 1 to 16 symbols). A recent trend is towards VHDL or Verilog designs (logic cores or intellectual property cores). These have a number of advantages over standard ICs. A logic core can be integrated with other VHDL or Verilog components and synthesized to an FPGA (Field Programmable Gate Array) or ASIC (Application Specific Integrated Circuit) – this enables so-called "System on Chip" designs where multiple modules can be combined in a single IC. Depending on production volumes, logic cores can often give significantly lower system costs than "standard" ICs. By using logic cores, a designer avoids the potential need to do a "lifetime buy" of a Reed-Solomon IC.
Software Implementation
Until recently, software implementations in "real-time" required too much computational power for all but the simplest of Reed-Solomon codes (i.e. codes with small values of t). The major difficulty in implementing Reed-Solomon codes in software is that general purpose processors do not support Galois field arithmetic operations. For example, to implement a Galois field multiply in software requires a test for 0, two log table look-ups, modulo add and anti-log table look-up. However, careful design together with increases in processor performance mean that software implementations can operate at relatively high data rates. The following table gives some example benchmark figures on a 166MHz Pentium PC:
| Code | Data rate |
| RS(255,251) | 12 Mbps |
| RS(255,239) | 2.7 Mbps |
| RS(255,223) | 1.1 Mbps |
These data rates are for decoding only: encoding is considerably faster since it requires less computation.
5. Further reading
In this paper we have deliberately avoided discussing the theory and implementation of Reed-Solomon codes in detail. For more detail please see the following books:
1.Wicker, "Error Control Systems for Digital Communication and Storage", Prentice-Hall 1995
2. Lin and Costello, "Error Control Coding: Fundamentals and Applications", Prentice-Hall 1983
3. Clark and Cain, "Error Correction Coding for Digital Communications", Plenum 1988
4. Wilson, "Digital Modulation and Coding", Prentice-Hall 1996
6. About the authors
This paper was written by Martyn Riley and Iain Richardson. For more details about the authors click here.
Copyright © 4i2i Communications Ltd 1996, 1997, 1998