Formal Foundations for Intermittent Concurrency
Imagine that you program satellites for NASA that orbit the moon. These satellites are programmed remotely from Earth as the inaccessibility of space makes manual device maintenance (e.g. regular battery replacement) infeasible. Instead of batteries, these satellites are equipped with solar panels that power computations. A program executes when energy is available, halts its computation when energy is depleted (e.g., when satellites are blocked from the sun’s rays), and re-executes when more energy is retrieved. These satellites rely on a combination of volatile memory , which is erased in the event of a power failure, and nonvolatile memory , which instead persists.
This is a classic example of an intermittent system which computes in harsh or inaccessible environments, e.g., tiny satellites in space [6], wildlife monitors [5], and smart civil infrastructure [1]. Due to the real-time nature of these applications, deploying buggy code could have irreversible and potentially harmful consequences. Hence, ensuring the correctness of these systems prior to runtime is essential.
To make progress and compute correct results despite such power failures, the runtime system must copy sufficient state into checkpoints prior to power failure to be restored upon reboot. In particular, state-of-the-art intermittent systems use a combination of just-in-time (JIT) checkpointing , which saves all of volatile state just before power failure and resumes from the line of failure upon reboot, and atomic regions , which checkpoint variables at the start of their execution and re-execute from the beginning.
The problem with running sequential programs intermittently
Without care, re-execution of atomic regions can introduce consistency errors. Because updates to nonvolatile memory do not clear on power failure, some code patterns are inherently non-idempotent : executing such code multiple times yields a different result compared to a single, continuously-powered execution. To illustrate a potential memory consistency bug in a sequential intermittent program, consider the program and its example executions below:

The left side of the figure shows an atomic region where the variable \(d\) is assigned the difference between \(prev\) and \(x\), and then \(prev\) is assigned the value of \(x\). Suppose the initial nonvolatile memory state is 3, 0, 5, and that no variables are checkpointed, as in (a). The assignments write 2 to \(d\), and then 3 to \(prev\). If power fails immediately after the assignment to \(prev\) but before the end of the atomic region, the program will re-execute from the beginning with the state 3, 2, 3. However, on this re-execution, the assignment to \(d\) which reads the value of \(prev\) from the prior execution stores 0, resulting in an incorrect final state: one that does not match the expected final state of any continuously-powered execution of the same program, which should be 3, 2, 3. The variable \(prev\) is involved in a write-after-read (WAR) pattern, which is one of the causes of memory consistency bugs.
To execute the program correctly, checkpointing and restoring nonvolatile memory is required. Prior work shows that checkpointing only variables involved in non-idempotent code patterns, e.g. WAR patterns, which is more performant than checkpointing all of nonvolatile state, is sufficient to enable correct intermittent execution. In our example, it suffices to checkpoint only \(prev\), as shown in (b). Upon entering the atomic region, the runtime system would checkpoint \(prev\), storing a copy of its initial value 5 in a checkpoint \(prev^{ck}\). Upon reboot from power failure, the checkpointed value from \(prev^{ck}\) refreshes the value of \(prev\), so that the assignment to \(d\) correctly results in 2, and the desired final state is obtained: 3, 2, 3.
The problem with running concurrent programs intermittently
Like most embedded systems applications, the programs running on your satellites are concurrent in nature, consisting of a combination of software-sheduled events and time-sensitive hardware-triggered interrupts that access shared variables. These tasks are annotated with a priority number, and only tasks with a higher priority than the currently-running process can interrupt it. To protect against data races, critical sections envelop accesses to shared variables and are assigned a priority that is high enough to prevent interruption from other tasks.
For example, your latest program (shown below) takes temperature readings and computes the difference between consecutive readings.
TASK1(pr:1, sh:x): ISR_IN(pr:2, sh:x)(inp):
atomic(prev) { crit(pr:2) {
crit(pr:2) { x := inp
d := diff(prev,x) x := tofahren(x)
prev := x }
}
return2station(d)
}
The work is split between a software-scheduled event, TASK1, and an interrupt handler ISR_IN that fires whenever the sensor peripheral is ready. TASK1 reads \(x\), the most recent input value, stores the difference between \(x\) and \(prev\) in \(d\), and updates \(prev\) with \(x\). The process \(\mathsf{return2station}\) causes the satellite to halt its orbit and begin traveling back to Earth if the difference \(d\) between readings is neglible. Whereas the call to \(\mathsf{return2station}\) relies only on accesses to local variable \(d\), the assignments to \(d\) and \(prev\) rely on shared variable \(x\), and hence must be wrapped inside a critical section. Whenever it fires, ISR_IN stores the sensor input from \(inp\) into \(x\) and converts it to degrees Fahrenheit. In the event of a power failure, ISR_IN would completely abandon its execution and not resume (due to its time-sensitivity), whereas TASK1 would re-execute from the beginning (due to its atomic region).
To guarantee that the satellites would operate as intended (and not make a surprise trip home to Earth), it is crucial that the programs running on these satellites are verified to be correct : every intermittent execution of that program should have a corresponding continuously-powered execution resulting in the same final state when provided the same initial state.
To see this, we examine execution traces of this program, shown below.
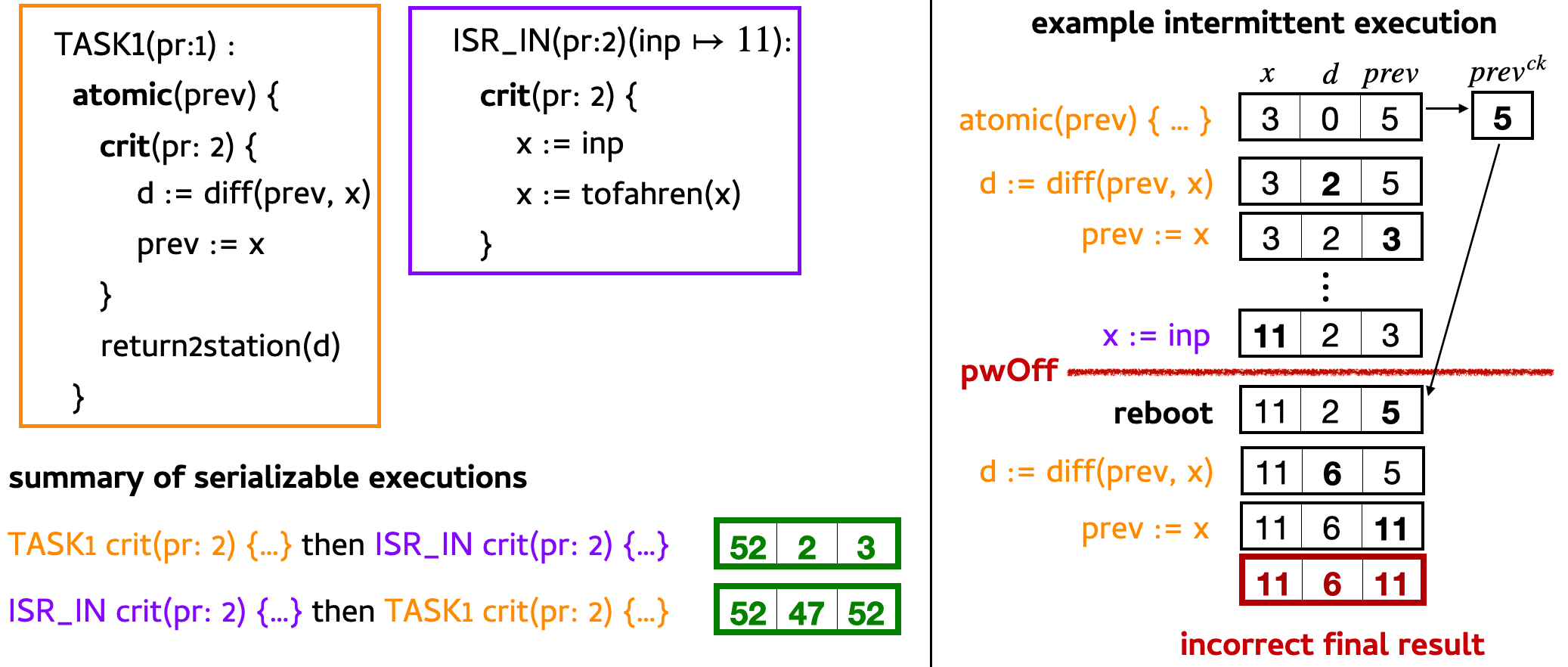
Again, suppose that the initial state of \(x\), \(d\), and \(prev\) is 3, 0, 5. First, we consider a possible intermittent execution of this program shown on the right. Execution begins in TASK1. Like before, \(prev\) is checkpointed. After entering the critical section, the difference between \(prev\) and \(x\), which is 2, is stored in \(d\). Then, \(prev\) is updated to the value of \(x\) which is 3. Immediately after the critical section, ISR_IN preempts TASK1 to update \(x\) with a new sensor reading 11. Now the state is 11, 2, 3. Suppose that power fails immediately after, and before ISR_IN finishes executing. Upon reboot, the runtime system recovers the checkpointed value from \(prev^{ck}\), and TASK1 re-executes from the beginning on the state 11, 2, 5. The difference is re-computed, this time storing the value 6 in \(d\), and 11 in \(prev\). ISR_IN does not re-execute, so the final state is 11, 6, 11.
To attempt to show that this program is correct, we need to find a continuously-powered execution of it that produces the same final state when provided the same initial state. The two serial orderings are that TASK1’s critical section executes first, followed by the ISR_IN’s, and vice-versa. Assuming TASK1’s is first, the critical section sets \(d\) to 2, and \(prev\) to 3. Then, ISR_IN fires, obtaining an input value for \(x\) and then converting it to degrees Fahrenheit: 52. TASK1 resumes its execution, and the final memory state is 52, 2, 3. Alternatively, if the interrupt fires first, the handler sets \(x\) to 11, and then performs the conversion to degrees Fahrenheit, setting \(x\) to 52. When TASK1 executes, it sets \(d\) to 47 and \(prev\) to 52, resulting in the final memory state 52, 47, 52. Any other result, like one that ends with \(d\) set to 6, would be both incorrect and impossible!
While prior work provides rich correctness guarantees for sequential intermittent program execution [3,4,8,10], support for intermittent execution of concurrent programs (like the one above) has lagged. The few works that do exist assume rigid programming models (e.g., programs never re-execute, devices cannot access volatile memory, tasks must not freely access shared memory) and lack formal correctness guarantees [2,7,11].
Key ideas of our solution
This blog post outlines the key ideas behind a co-designed runtime system and type system. Our system ensures that programs that type check are guaranteed to execute correctly at runtime.
Modular programming and flexible re-execution policies
To overcome the limitations of prior work, our system supports tasks that adopt a broad spectrum of re-execution behaviors, which we refer to as re-execution policies ; they range from tasks with JIT and atomic regions [3,4,10] which continue their execution immediate -ly, to those that are completely discard -ed (as in time-sensitive interrupts, like ISR_IN), to those that run an alternative (perhaps more energy-efficient) version of the original task. Our system supports any chaining of these re-execution policies, e.g., failing a discard task and then attempting an alternative with a re-executable atomic region that eventually finishes executing.
Local and global (non-)idempotence
Our re-execution policies work in conjunction with a static type system that describes expected (non-)idempotence of data values. The key insight is that variables written by discard tasks, whose values may differ across re-executions, are non-idempotent , and must not interfere with idempotent data, which are expected to be the same across executions. Prior work uses type qualifiers to label variables as idempotent \((\mathsf{Id})\) and non-idempotent \((\mathsf{Nid})\), and employs an information flow type system to enforce that non-idempotent data does not interfere with idempotent results [10].
In the program above, \(\mathsf{x}\) is idempotent in TASK1, but may depend on the non-idempotent writes from ISR_IN, therefore violating the mentioned policy. To statically catch such potential dependencies, our type system describes and reasons about variable (non-)idempotence with respect to both local usage within a given task and also global usage by other tasks in the system. For global usage, we consider effects from tasks with higher priority versus lower or equal priority separately. The rationale for this distinction is the following: tasks with a strictly higher priority could preempt the local task, whereas tasks with a lower or equal priority instead could have been preempted . In either case, non-idempotent updates to shared variables could be caused in different ways. Therefore, our types consist of triples of type qualifiers \(\mathtt{\langle qlocal, qleq, qhigh\rangle}\), where \(\mathtt{qlocal}\) represents the local (non-)idempotence of a variable, and \(\mathtt{qleq}\) and \(\mathtt{qhigh}\) represent its (non-)idempotence with respect to effects from tasks of lower or equal priority and higher priority, respectively, from the perspective of the local task.
Our static typing, which checks each task separately under its own typing context , therefore, must check that non-idempotent data, whether it be coming from local or global sources, could not violate local idempotency requirements.
Type checking the running example
Below, we highlight key aspects of type checking the example program from above. We provide its task specifications, and show how to use them to build a typing context that describes (non-)idempotence for each variable in a task. We then show how our type checking can statically detect that the program above is incorrect, and explain how our system would fix it. Programs that pass our type checking are guaranteed to execute correctly before they are actually deployed.
Step 0: define a specification for each task
Intentionally similar to popular frameworks for continuous, interrupt-driven concurrency (e.g., RTIC ), a user of our system writes their program as a collection of tasks, including interrupts and events. Below, we provide an (initial) specification for each task in the example program, consisting of a priority \(\mathsf{pr}\) (e.g., 1 or 2), re-execution policy \(\mathsf{rPol}\) (e.g., immediate or discard ), and set of shared variables accessed by the task \(\mathsf{ShAcc}\) (e.g., \(x\)). As in prior work [10], each atomic region is additionally annotated with sets of idempotent variables in an atomic region: checkpointed CP (e.g., \(prev\)), read-only RD (e.g., \(x\)), and must-first-write MFW (e.g., \(d\)).

Our static type checking checks whether the programmer’s task specifications can be met. Towards doing so, our system uses these annotations to build typing contexts for checking each task, which we discuss next.
Step 1: build typing contexts according to the specification
In order to check whether a program is correct, we need to construct a typing context \(\Gamma\) for each task according to its specification. For each variable accessed by a task, the typing context provides its type consisting of idempotence qualifiers \(\mathtt{\langle qlocal, qleq, qhigh\rangle}\), where the first component \(\mathtt{qlocal}\) represents the local (non-)idempotence of a variable, and the second and third components \(\mathtt{qleq}\) and \(\mathtt{qhigh}\) represent global (non-)idempotence as described above.
We highlight the key observations involved in constructing a typing context below:
- checkpointed variables should be idempotent across all tasks, as that data is always expected to be the same on each (re-)execution.
- variables written by discard tasks should be non-idempotent from the perspective of other tasks, as the values stored in those locations may not be the same across intermittent and continuously-powered executions.
- atomic region variables CP , RD , MFW are locally idempotent.
- task inputs, which are considered local to a task and are the same on every (re-)execution of a task, are fully idempotent.
Using this schema, we now construct typing contexts \(\Gamma_\mathsf{T1}\) and \(\Gamma_\mathsf{IN}\) for tasks TASK1 and ISR_IN according to the task specifications above (initially represented by ?, and gradually \(\color{red}\text{filled in}\color{black}\)).
\(\Gamma_\mathsf{T1} = {d : \mathsf{int}@\langle ?,?,? \rangle, x : \mathsf{int}@\langle ?,?,? \rangle, \mathit{prev} : \mathsf{int}@\langle ?,?,? \rangle}\)
\(\Gamma_\mathsf{IN} = {x : \mathsf{int}@\langle ?,?,? \rangle, \mathit{inp} : \mathsf{int}@\langle ?,?,? \rangle}\)
First, the variable \(prev\), which is checkpointed in TASK1’s atomic region, must be locally and globally idempotent (i.e. has type \(\mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Id} \rangle\) in \(\Gamma_\mathsf{T1}\)). The variables \(x\) and \(d\), which are included in the RD and MFW sets of the atomic region, are locally idempotent. Since there are no lower priority tasks in the system, the second qualifier of \(x\) in \(\Gamma_\mathsf{T1}\) defaults to \(\mathsf{Id}\). The variable \(d\), which is local to TASK1 and is not shared with other tasks, has both second and third qualifiers \(\mathsf{Id}\) in \(\Gamma_\mathsf{T1}\).
\(\Gamma_\mathsf{T1} = {d : \mathsf{int}@\langle \mathsf{\color{red}Id},\mathsf{\color{red}Id},\mathsf{\color{red}Id} \rangle, x : \mathsf{int}@\langle \mathsf{\color{red}Id},\mathsf{\color{red}Id},? \rangle, \mathit{prev} : \mathsf{int}@\langle \mathsf{\color{red}Id},\mathsf{\color{red}Id},\mathsf{\color{red}Id} \rangle}\)
\(\Gamma_\mathsf{IN} = {x : \mathsf{int}@\langle ?,?,? \rangle, \mathit{inp} : \mathsf{int}@\langle ?,?,? \rangle}\)
The remainder of \(x\)’s type in \(\Gamma_\mathsf{T1}\) depends on how \(x\) is accessed by higher-priority tasks that share it: ISR_IN. Since ISR_IN is a discard task that writes \(x\), the third qualifier of \(x\) in \(\Gamma_\mathsf{T1}\) is \(\mathsf{Nid}\); similarly, the local qualifier of \(x\) in \(\Gamma_\mathsf{IN}\) is \(\mathsf{Nid}\).
\(\Gamma_\mathsf{T1} = {d : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Id} \rangle, x : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{\color{red}Nid} \rangle, \mathit{prev} : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Id} \rangle}\)
\(\Gamma_\mathsf{IN} = {x : \mathsf{int}@\langle \mathsf{\color{red}Nid}, ?, ? \rangle, \mathit{inp} : \mathsf{int}@\langle ?,?,? \rangle}\)
With \(\Gamma_\mathsf{T1}\) complete, we continue to fill in the remaining missing qualifiers in \(\Gamma_\mathsf{IN}\). As there are no tasks with higher priority than ISR_IN, the third qualifier of \(x\) in \(\Gamma_\mathsf{IN}\) is \(\mathsf{Id}\). Since TASK1 is the only task with lower priority than ISR_IN, the second qualifier of \(x\) in \(\Gamma_\mathsf{IN}\) comes from the first qualifier of \(x\) in \(\Gamma_\mathsf{T1}\), which is \(\mathsf{Id}\). Since we assume that task inputs are the same on re-execution, \(inp\) is locally and globally idempotent in \(\Gamma_\mathsf{IN}\). We arrive at the following typing contexts:
\(\Gamma_\mathsf{T1} = {d : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Id} \rangle, x : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Nid} \rangle, \mathit{prev} : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Id} \rangle}\)
\(\Gamma_\mathsf{IN} = {x : \mathsf{int}@\langle \mathsf{Nid},\mathsf{\color{red}Id},\mathsf{\color{red}Id}\rangle, \mathit{inp} : \mathsf{int}@\langle \mathsf{\color{red}Id},\mathsf{\color{red}Id},\mathsf{\color{red}Id} \rangle}\)
Step 2: check that the specification can be satisfied
Using these typing contexts, we can now check whether the example program is correct relative to its specification. Two of the most important checks performed by our typing rules are that:
- a given critical section cannot be preempted by any task that accesses common shared variables , and
- non-idempotent data does not flow to locally idempotent results .
The first is enforced by checking that the priority of each critical section is at least as high as the ceiling priority of any tasks that access common shared variables, as in the priority ceiling protocol frequently used in real-time systems [9]. The second is enforced by applying principles from information flow type systems, as described above: non-idempotent data from local and global sources must not flow to locally idempotent variables.
Below, we highlight key aspects of checking TASK1 and ISR_IN using the contexts \(\Gamma_\mathsf{T1}\) and \(\Gamma_\mathsf{IN}\).

We begin with checking ISR_IN under \(\Gamma_\mathsf{IN}\). As required by the first criterion, the priority of ISR_IN’s critical section (i.e., 2) is as high as the ceiling priority of any tasks that access common shared variables (i.e., ISR_IN and TASK1). Obeying the second criterion, the assignments on Lines 11 and 12 each flow non-idempotent data to a locally non-idempotent variable.
Now, we check TASK1. Again, the first criterion is upheld by the critical section, whose priority of 2 bounds the ceiling priority of sharing tasks TASK1 and ISR_IN. However, the assignments inside the critical section fail to uphold the second criterion: the assignments on Lines 4 and 5 flow non-idempotent data from \(x\) to locally idempotent variables \(d\) and \(prev\). At this point, type checking fails, indicating that the program could execute incorrectly at runtime.
Task-level checkpointing is necessary for correctness
The problem with the program above is that the non-idempotent value of \(x\) from ISR_IN is reverted after reboot. There are many similar scenarios where completely ruling out this kind of program is too restrictive. One key insight is that rather than disallowing such programs, the runtime system should subvert the effects of discard tasks, like \(x\) in ISR_IN. That is a failed discard task should behave as if it never happened. To erase the effects of \(x\)’s writes from ISR_IN’s failed execution, the runtime system should provide a stable checkpointed version of it to revert to upon reboot.
To help programs like the one above execute correctly, we introduce task-level checkpointing which allows tasks with discard policy to checkpoint variables at the beginning of their execution. If power fails before the task finishes, writes by the task would be reverted, similar to checkpointing in atomic regions but without re-execution. Since power failure could occur at any point, the checkpointed context must always contain only stable (idempotent) data, and hence the runtime system must only update checkpoints at particular points of a task’s execution depending on its re-execution policy: on every write for JIT regions (which are stable), and at the beginning and successful conclusion of an atomic region and discard task execution.
Task-level checkpointing: program execution
We show the execution of the program above but where ISR_IN checkpoints \(x\) at the beginning of its execution.

As before, TASK1 executes until its critical section completes, at which point ISR_IN fires. At the beginning of ISR_IN’s execution, it makes a checkpointed copy of \(x\)’s initial value of 3 in \(x^{ck}\). The input 11 is assigned to \(x\). Then power fails. Upon reboot, the checkpointed values stored in \(x^{ck}\) and \(prev^{ck}\) refresh the values of \(x\) and \(prev\) in nonvolatile memory, and TASK1 re-executes on the state 3, 2, 5. The assignments update \(d\) to 2, and \(prev\) to 3, resulting in the expected final state: 3, 2, 3. This final state is correct, as it matches a single execution of TASK1.
Task-level checkpointing: program specifications and type checking
We augment our task specifications with a task-level set of checkpointed variables ShCP , indicating which variables to checkpoint at the task level, e.g., \(x\) in ISR_IN. Checkpointing \(x\) in ISR_IN changes its local qualifier in \(\Gamma_\mathsf{IN}\) to \(\mathsf{Id}\), since checkpointed variables are fully idempotent. Likewise, the third qualifier in \(\Gamma_\mathsf{T1}\) is also updated to \(\mathsf{Id}\). The updated contexts are shown below with revisions \(\color{red}\text{highlighted}\color{black}\):
\(\Gamma_\mathsf{T1} = {d : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Id} \rangle, x : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{\color{red}Id} \rangle, \mathit{prev} : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Id} \rangle}\)
\(\Gamma_\mathsf{IN} = {x : \mathsf{int}@\langle \mathsf{\color{red}Id},\mathsf{Id},\mathsf{Id}\rangle, inp : \mathsf{int}@\langle \mathsf{Id},\mathsf{Id},\mathsf{Id}\rangle}\)
The updated type checking is outlined below.

This time, type checking succeeds: in TASK1, the assignments on Lines 4 and 5 flow idempotent data from \(x\) to locally idempotent variables \(d\) and \(prev\).
Closing remarks
This blog post is based on joint work with Milijana Surbatovich, Limin Jia, and Brandon Lucia. Our work introduces the first provably correct co-designed runtime system and typing rules for concurrent, intermittent programs. This blog post focused on the latter – how to detect whether a program will execute correctly prior to runtime.
In future extensions, we plan to support software-scheduled events posted from atomic regions and discard tasks. If treated naively, the re-execution of atomic regions could cause the same event to be posted over and over again on each re-execution, and discard tasks could post events before abaondoning execution due to power failure while writing to shared variables. In both cases, ensuring that correctness is still upheld, i.e., finding a continuously-powered execution that corresponds to the intermittent execution, becomes even more precarious.
Our paper Towards a Formal Foundation for Intermittent Concurrency is currently under review, and we hope to share it soon.
Citations
[1] Adkins, J., Campbell, B., Ghena, B., Jackson, N., Pannuto, P., and Dutta, P. 2016. The Signpost Network: Demo Abstract. In Proceedings of the 14th ACM Conference on Embedded Network Sensor Systems CD-ROM (Stanford, CA, USA) (SenSys ’16). https://doi.org/10.1145/2994551.2996542
[2] Branco, A., Mottola, L., Alizai, M.H., and Siddiqui, J.H. 2019. Intermittent asynchronous peripheral operations. In Proceedings of the 17th Conference on Embedded Networked Sensor Systems (SenSys ’19). Association for Computing Machinery, New York, NY, USA, 55–67. https://doi.org/10.1145/3356250.3360033
[3] Farzaneh Derakhshan, Dotzel, M., Surbatovich, M., Jia, L. (2023). Modal Crash Types for Intermittent Computing. In: Wies, T. (eds) Programming Languages and Systems. ESOP 2023. Lecture Notes in Computer Science, vol 13990. Springer, Cham. https://doi.org/10.1007/978-3-031-30044-8_7
[4] Dotzel, M., Derakhshan, F., Surbatovich, M., and Jia, L.. 2025. Modal Crash Types for WAR-Aware Intermittent Computing. ACM Trans. Program. Lang. Syst. 47, 2, Article 5 (June 2025), 62 pages. https://doi.org/10.1145/3716311
[5] Nardello, M., Desai, H., Brunelli, D., and Lucia, B.. 2019. Camaroptera: A Batteryless Long-Range Remote Visual Sensing System. In Proceedings of the 7th International Workshop on Energy Harvesting & Energy-Neutral Sensing Systems (New York, NY, USA) (ENSsys’19). ACM, New York, NY, USA, 8–14. https://doi.org/10.1145/3362053. 3363491
[6] NASA (2022, October) KickSat-2. NASA Space Science Data Coordinated Archive. https://nssdc.gsfc.nasa.gov/nmc/spacecraft/display.action?id=2018-092G. Visited August 15th, 2025.
[7] Ruppel, E. and Lucia, B.. 2019. Transactional concurrency control for intermittent, energy-harvesting computing systems. In Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI 2019). Association for Computing Machinery, New York, NY, USA, 1085–1100. https://doi.org/10.1145/3314221.3314583
[8] Surbatovich, M., Lucia, B., and Jia, L.. 2020. Towards a Formal Foundation of Intermittent Computing. Proc. ACM Program. Lang. 4, OOPSLA, Article 163 (Nov. 2020), 31 pages. https://doi.org/10.1145/3428231
[9] Sha, L., Rajkumar, R., Lehoczky, J.: Priority inheritance protocols: an approach to real-time synchronization. IEEE Transactions on Computers 39(9), 1175–1185 (1990). https://doi.org/10.1109/12.57058
[10] Surbatovich, M., Spargo, N., Jia, L., and Lucia, B. 2023. A Type System for Safe Intermittent Computing. Proc. ACM Program. Lang. 7, PLDI, Article 136 (June 2023), 25 pages. https://doi.org/10.1145/3591250
[11] Yıldız, E., Chen, L., and Yıldırım, K.S. 2022. Immortal Threads: Multithreaded Event-driven Intermittent Computing on Ultra-Low-Power Microcontrollers. In 16th USENIX Symposium on Operating Systems Design and Implementation (OSDI 22). USENIX Association, Carlsbad, CA, 339–355. https://www.usenix.org/conference/osdi22/ presentation/yildiz