Connecting Automatic and Interactive Theorem Proving
The field of formal verification is all about using mathematically rigorous techniques and tools to prove properties about systems. The applications of formal verification vary widely. There are computer-checked correctness proofs for critical pieces of software such as compilers and microkernels , there are tools to help automatically verify specifications for arbitrary programs written in languages such as Rust , C , and OCaml , and there are even efforts to formally verify the safety of cyber-physical systems such as train controllers .
The common factor shared by each of these projects is the set of methods used to achieve their guarantees. Fundamentally, any formal verification project involves expressing a logical specification and then proving that specification is correct. There are two main ways to do this: automatically and interactively.
In this blog post, I’ll describe these two approaches, the tradeoffs between them, and close with some ways they can be used synergistically.
Automatic Theorem Proving
Automatic theorem provers are tools designed to accept formulas in some fixed logic as input and then, without any human assistance, establish whether the formula is satisfiable in the prover’s logic. The question of whether some formula \( F \) is unsatisfiable is equivalent to the question of whether its negation \( \neg F \) is valid, so if the goal is to prove the validity of some specification, it suffices to have a tool that can check satisfiability.
In addition to establishing whether formulas are satisfiable, automatic theorem provers also typically generate certificates of correctness demonstrating that their results are accurate. For satisfiable formulas, this certificate can take the form of a model , or set of assignments showing how the formula can be made true. For unsatisfiable formulas, this certificate can take the form of a structured proof which uses predefined rules to show how the original formula entails a contradiction.
The specifics of how automatic theorem provers are implemented, what their models look like, and how reliably their unsatisfiability proofs can be checked depend on which logic the automatic theorem prover supports. Automatic theorem provers for basic propositional logic can output proof formats that can be efficiently and reliably checked, but it is generally more difficult to efficiently and reliably check proof formats for more expressive logics.
Interactive Theorem Proving
Like automatic theorem provers, interactive theorem provers are tools designed to reason about formulas in some fixed logic. But unlike automatic theorem provers, interactive theorem provers don’t generally establish the validity or satisfiability of formulas on their own. Instead, they provide an interface by which users can write their own programs to generate proofs of formula validity.
In addition to providing an interface for users to reason about formulas, interactive theorem provers come with kernels which can check the correctness of proofs generated by its users. These correctness checks are generally built into the interactive theorem prover’s type system so that if a user can write a program whose type corresponds to some formula, then the typechecker will guarantee that the corresponding formula is valid.
The specifics of how interactive theorem provers are implemented and what their proofs look like vary from one interactive theorem prover to the next. There are some interactive theorem provers which require users to write their proofs in great detail with high levels of specificity, while others allow users to simply indicate large steps and provide automation to take care of the finer details. But regardless of the specificity with which users express their proofs, almost all interactive theorem provers are able to verify the correctness of its proofs with extremely high levels of confidence because the burden to actually generate the proofs is moved onto the user.
Tradeoffs Between the Two Technologies
Both automatic theorem proving and interactive theorem proving have their respective pros and cons.
Automatic Theorem Proving:
| Pros | Cons |
|---|---|
| The fact that users don’t need to write proofs creates a lower barrier for entry. | When a user is an expert or has some insight on how to solve a particular problem, it can be difficult to help or guide the prover. |
| Automatic theorem provers are optimized for efficiency, so when they can solve a problem, they can almost always do so much more quickly than a human. | The proofs generated by automatic theorem provers can be extremely difficult for humans to follow, and only some logics have proof formats that can be efficiently verified with high levels of confidence. |
| There are automatic theorem provers for a wide variety of logics, so users can choose to express their problem in the logic that is most appropriate or convenient. | The manner in which a user encodes their problem into logic can have a significant impact on the prover’s ability to solve it. |
| Automatic theorem provers are effective tools for solving large numbers of small problems or for solving arbitrary instances of a problem that can be encoded into logic. | Automatic theorem provers’ solutions can be brittle, so slight changes in how problems are generated can cause the prover to fail where it may have otherwise succeeded. |
Interactive Theorem Proving
| Pros | Cons |
|---|---|
| Interactive theorem provers provide expert users more control over how a problem is solved or how a proof is generated. | The fact that users are forced to write their own proofs creates a much higher barrier for entry. |
| The process of manually formalizing mathematical proofs can expose bugs in previously accepted arguments and increase understanding of the problem’s solution. | The process of manually proving theorems can be extremely tedious, even with supporting automation. |
| Interactive theorem provers operate on more expressive logics, which tends to make encoding a problem into an interactive theorem prover easier than encoding the same problem into an automatic theorem prover. | The expertise and effort required to encode problems well isn’t eliminated in interactive theorem provers. It is just moved over to the process of actually proving it. |
| Interactive theorem provers are (usually) designed to ensure that there is only a small trusted codebase (TCB) that needs to be bug-free to guarantee the soundness of the interactive theorem prover’s results. This small TCB increases the confidence with which the prover can guarantee its results. | For many use cases, the level of confidence afforded by interactive theorem provers isn’t actually necessary. In some domains, there are additional means of increasing confidence, and often, having a tool that actually solves the problem can be more important. |
Summarizing the above, we see that the use of an interactive theorem prover typically constitutes a greater investment in time, energy, and expertise, but they can be used to prove more complicated facts with higher levels of confidence (because the correctness of the final result depends on a smaller TCB being bug-free). When the goal is to verify the correctness or safety of a single critical system, interactive theorem provers will generally be preferred. When the goal is to support nonexperts or solve arbitrary instances from a class of similar problems, automatic theorem provers will generally be preferred. Of course, there are exceptions to both of these generalizations, such as when automatic theorem provers are used to discover solutions to previously unsolved math problems or interactive theorem provers are used to verify procedures that can solve arbitrary problems from a particular class .
But there’s no reason we need to only choose one tool or the other. There are lots of ways in which automatic and interactive theorem provers have been used jointly to complement one another.
Using Automatic and Interactive Theorem Provers Together
There are a wide variety of ways in which automatic and interactive theorem provers have been used together. Here, I describe some ways the two technologies have been used synergistically. Although these examples are by no means exhaustive, they are intended to illustrate a reasonable diversity of modern methods.
1. Using an interactive theorem prover to verify a less expressive logic’s encoding:
The logics supported by interactive theorem provers tend to be much more expressive than the logics supported by automatic theorem provers, and automatic theorem provers’ abilities to solve problems can be sensitive to how the problems are encoded. Because of this, leveraging automatic theorem provers to solve difficult problems can require very careful and sometimes very complicated encodings. A wide variety of tricks are employed to simplify problems before they are even translated into formulas, and more tricks are still used to manipulate translated formulas into a format that is maximally convenient for an automatic theorem prover.
Because of this, even after an automatic theorem prover is successfully used to establish whether a formula is satisfiable, one can question whether the formula still accurately represents the original specification or problem it was meant to encode. After all, who’s to say that some error wasn’t introduced over the course of the many manipulations that were performed to simplify the original problem?
To restore confidence in the correctness of an encoding, even after many iterations of simplification and manipulation, we can use an interactive theorem prover’s expressive logic to define an extremely straightforward and obviously correct encoding of the original problem. Then, the set of the manipulations that were performed to obtain a more efficient encoding can be defined in the interactive theorem prover, and the soundness of those manipulations can be proven. In the end, the interactive theorem prover will yield a proof that the obviously correct encoding is equivalent to the more complicated and efficient encoding, allowing us to apply the automatic theorem prover’s results to the straightforward encoding (and therefore, to the original problem/specification). One example of this approach can be seen in the formal verification of the empty hexagon number which formalizes the reduction of a geometric problem in Lean to the unsatisfiability of a propositional formula.
2. Using an automatic theorem prover to catch mistakes during interactive theorem proving:
In order to prove a theorem, it generally helps for the theorem to actually be true. Of course, nobody intentionally sets out to try to prove facts they know to be false, but typos, missing assumptions, and misunderstandings can easily cause an interactive theorem prover user to create unprovable goals by accident. Due to the complexity of formal verification and the many levels of abstraction that have to be traversed in order to formally prove theorems, it is not uncommon for users to waste nontrivial amounts of time trying to prove theorems that are in fact false.
Earlier, I said that a formula \( F \) is unsatisfiable if and only if its negation \( \neg F \) is valid. By the same token, a theorem is invalid if and only if its negation is satisfiable. So to check whether an invalid theorem has accidentally been created, one can check whether an automatic theorem prover is able to satisfy its negation. This is what Nitpick does.
Here is an example of what one might see if they used Nitpick in the interactive theorem prover Isabelle/HOL .
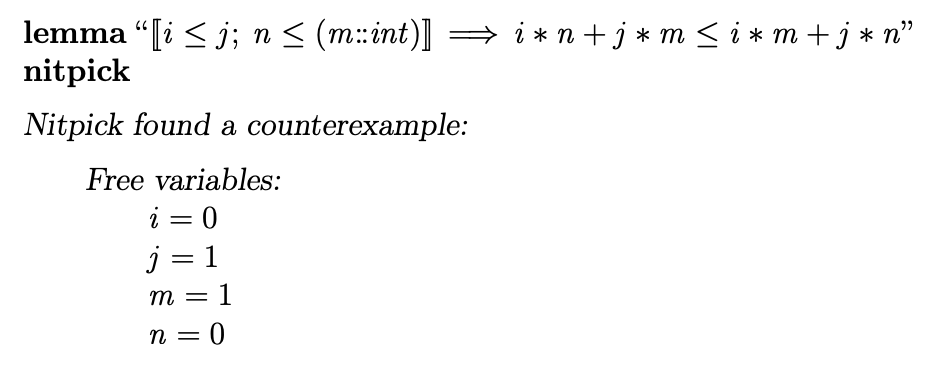
Not only does Nitpick identify that the relevant lemma is false, it is also able to provide a concrete counterexample demonstrating why it is false. Under the hood, Nitpick is translating the original lemma into a formula that can be accepted by the automatic theorem prover Kodkod , asking whether the formula’s negation is satisfiable, and using the model output by Kodkod to generate the counterexample we see above. Nitpick helps users catch errors early, preventing them from wasting time struggling in vain to prove impossible theorems.
3. Using an automatic theorem prover to distinguish necessary and unnecessary assumptions:
Because formal proofs require significant amounts of explicit detail, it is common for interactive theorem provers to be supplemented with automation capable of finding small proofs for simple goals. Having this automation enables users to focus on the bigger picture, leaving small and unimportant details for the computer to figure out.
But since interactive theorem provers typically require much more detailed proofs than automatic theorem provers, the automation included in state-of-the-art interactive theorem provers is almost always weaker than the automation afforded by state-of-the-art automatic theorem provers. This holds even for automation like Metis and Duper which explicitly utilize some of the techniques implemented in state-of-the-art automatic theorem provers.
A common pain point in an interactive theorem prover’s automation is determining which of the thousands of accessible library facts should be considered while searching for a proof. One way to effectively make use of an interactive theorem prover’s automation, even in the presence of thousands of plausibly relevant library facts, is to leverage automatic theorem provers. Perhaps the most notable and widely used example of leveraging automatic theorem provers in an interactive theorem proving context is Isabelle’s Sledgehammer .
Isabelle’s Sledgehammer consists of three main steps. First, a premise selection tool is used to gather hundreds of facts from the library that might be relevant to the current goal. Isabelle’s built-in automation generally isn’t strong enough to effectively reason about so many facts, but automatic theorem provers are. So the second step is to translate the current goal and all of the gathered facts into a logic that can be accepted by an automatic theorem prover. If the automatic theorem prover is able to use the given facts to solve the goal, it can tell Sledgehammer which facts were actually needed in the final proof. Finally, this much smaller selection of facts can be provided to Isabelle’s built-in automation, and hopefully, the built-in automation will be able to find a proof in this smaller search space.
This procedure allows Sledgehammer to leverage automatic theorem provers’ efficiency to distinguish necessary and unnecessary assumptions in order to aid its internal automation. Notably, even though Isabelle itself may have a higher proof standard than some of the automatic theorem provers it calls, the reliability of the resulting proof isn’t compromised because the automatic theorem prover was only used as a filter. Its proofs don’t need to be trusted.
4. Using an interactive theorem prover to verify the results of an automatic theorem prover:
It’s nice that automatic theorem provers can help narrow the search for interactive theorem provers’ automation, but wouldn’t it be better to just use automatic theorem provers as automation for interactive theorem provers? After all, automatic theorem provers can already output structured proofs showing how unsatisfiable formulas entail contradictions.
Directly using an automatic theorem prover to produce proofs that can be accepted by an interactive theorem prover’s kernel requires more work than merely using it to discover a minimal set of relevant lemmas. But depending on the automatic theorem prover’s logic and the specificity of its proofs, it can be done. The main thing required, besides a translation between the two technologies’ logics, is to verify in the interactive theorem prover that all of the rules that the automatic theorem prover can output are sound. Each rule that appears in the automatic theorem prover’s structured proof can then be “replayed” in the interactive theorem prover, yielding a formal proof consisting only of rules proven to be sound. This approach is used to reconstruct veriT proofs in both Isabelle and Coq .
Although replaying the same proof in two technologies requires a significant amount of work (not only does the proof need to be found automatically, it also needs to be verified to the high standards imposed by interactive theorem provers), it allows us to combine the convenience and efficiency of automatic theorem provers with the high trustworthiness of interactive theorem provers.
Conclusion
We’ve now seen the tradeoffs between automatic and interactive theorem proving, and we’ve also seen a variety of ways the technologies can be used jointly to bolster each other’s strengths and cover each other’s weaknesses. I think there is a lot of promise in past and ongoing work that uses automatic theorem proving to make interactive theorem proving more convenient, and uses interactive theorem proving to reduce the trusted codebases for results obtained via automatic theorem proving.