Operations on Binary Search Tree’s

In the previous lesson, we considered a particular kind of a binary tree called a Binary Search Tree (BST). A binary tree is a binary search tree (BST) if and only if an inorder traversal of the binary tree results in a sorted sequence. The idea of a binary search tree is that data is stored according to an order, so that it can be retrieved very efficiently.

A BST is a binary tree of nodes ordered in the following way:

1. Each node contains one key (also unique)
2. The keys in the left subtree are < (less) than the key in its parent node
3. The keys in the right subtree > (greater) than the key in its parent node
4. Duplicate node keys are not allowed.

Here is an example of a BST

Exercise : Draw the binary tree which would be created by inserting the following numbers in the order given

  50   30   25   75   82   28   63   70   4   43   74   35

If the BST is built in a “balanced” fashion, then BST provides log time access to each element. Consider an arbitrary BST of the height k. The total possible number of nodes is given by

 k+1
2   - 1

In order to find a particular node we need to perform one comparison on each level, or maximum of(k+1) total. Now, assume that we know the number of nodes and we want to figure out the number of comparisons. We have to solve the following equation with respect to k:

Assume that we have a “balanced” tree with n nodes. If the maximum number of comparisons to find an entry is (k+1), where k is the height, we have

 K+1
2   - 1 = n

we obtain

k = log2(n+1) – 1 = O(log2n)

This means, that a “balanced” BST with n nodes has a maximum order of log(n) levels, and thus it takes at most log(n) comparisons to find a particular node. This is the most important fact you need to know about BSTs. But building a BST as a balanced tree is not a trivial task. If the data is randomly distributed, then we can expect that a tree can be “almost” balanced, or there is a good probability that it would be. However, if the data already has a pattern, then just naïve insertion into a BST will result in unbalanced trees. For example, if we just insert the data 1, 2, 3, 4, 5 into a BST in the order they come, we will end up with a tree that looks like this:

Binary search trees work well for many applications (one of them is a dictionary or help

browser). But they can be limiting because of their bad worst-case performance

height = O(# nodes). Imagine a binary search tree created from a list that is already sorted.

Clearly, the tree will grow to the right or to the left. A binary search tree with this worst-

case structure is no more efficient than a regular linked list. A great care needs to be

taken in order to keep the tree as balanced as possible. There are many techniques for

balancing a tree including AVL trees, and Splay Trees. We will discuss AVL trees in the

next lesson. Splay Trees will be discussed in advanced data structure courses like 15-211.

 
BST OPERATIONS
 There are a number of operations on BST’s that are important to understand. We will 
 discuss some of the basic operations such as how to insert a node into a BST, how to
delete a node from a BST and how to search for a node in a BST. 
 
 
Inserting a node
A naïve algorithm for inserting a node into a BST is that, we start from the root node, if 
the node to insert is less than the root, we go to left child, and otherwise we go to the 
right child of the root. We continue this process (each node is a root for some sub tree)
 until we find a null pointer (or leaf node) where we cannot go any further. We then insert 
the node as a left or right child of the leaf node based on node is less or greater than the 
leaf node. We note that a new node is always inserted as a leaf node. A recursive 
algorithm for inserting a node into a BST is as follows. Assume we insert a node N to
 tree T. if the tree is empty, the we return new node N as the tree. Otherwise, the 
problem of inserting is reduced to inserting the node N to left of right sub trees of T,
 depending on N is less or greater than T. A definition is as follows.
 
Insert(N, T)  = N   if T is empty
  = insert(N, T.left)  if  N < T
  = insert(N, T.right) if  N > T
 
 
Searching for a node
Searching for a node is similar to inserting a node. We start from root, and then go left or 
right until we find (or not find the node). A recursive definition of search is as follows. 
If the node is equal to root, then we return true. If the root is null, then we return false. 
Otherwise we recursively solve the problem for T.left or T.right, depending on N < T or
 N > T. A recursive definition is as follows.
 
Search should return a true or false, depending on the node is found or not.
Search(N, T) =  false   if T is empty
  =  true    if T = N
   = search(N, T.left) if N < T
  = search(N, T.right) if N > T
 
Deleting a node
  A BST is a connected structure. That is, all nodes in a tree are connected to some other 
 node. For example, each node has a parent, unless node is the root. Therefore deleting a 
 node could affect all sub trees of that node.  For example, deleting node 5 from the tree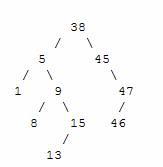
 

 
 could result in losing sub trees that are rooted at 1 and 9. Hence we need to be careful
 about deleting nodes from a tree. The best way to deal with deletion seems to be considering special cases. What if the node to delete is a leaf node? What if the node is a node with just one child? What if the node is an internal node (with two children). The latter case is the hardest to resolve. But we will find a way to handle this situation as well.
Case 1 : The node to delete is a leaf node
This is a very easy case. Just delete the node. We are done

 
Case 2 : The node to delete is a node with one child.
This is also not too bad. If the node to be deleted is a left child of the parent, then we connect the left pointer of the parent (of the deleted node) to the single child. Otherwise if the node to be deleted is a right child of the parent, then we connect the right pointer of the parent (of the deleted node) to single child.
 

 
 
Case 3: The node to delete is a node with two children
This is a difficult case as we need to deal with two sub trees. But we find an easy way to handle it. First we find a replacement node (from leaf node or nodes with one child) for the node to be deleted. We need to do this while maintaining the BST order property. Then we swap leaf node or node with one child with the node to be deleted (swap the data) and delete the leaf node or node with one child (case 1 or case 2)
 
Next problem is finding a replacement leaf node for the node to be deleted. We can easily find this as follows. If the node to be deleted is N, the find the largest node in the left sub tree of N or the smallest node in the right sub tree of N. These are two candidates that can replace the node to be deleted without losing the order property. For example, consider the following tree and suppose we need to delete the root 38.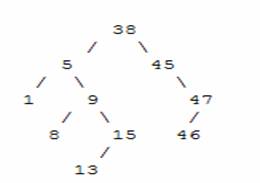

 
 
 
Then we find the largest node in the left sub tree (15) or smallest node in the right sub tree (45) and replace the root with that node and then delete that node. The following set of images demonstrates this process.