Linked Lists - Introduction

 

A List can be defined as an ordered collection of data. An array is a list of data that can be randomly accessed using an index. Arrays are static data structures and one disadvantage of using Arrays to store data is that Arrays cannot be extended or reduced to fit the data set.  Therefore it is possible that we may allocate too much or too little space depending on our speculation of the size of the data set. It is possible to resize the array when the array is full. But the operation requires, claiming new memory for the array and copying elements from the old array to the new array and destroying the old array. These are all expensive operations based on the size of the array. Arrays are also expensive to maintain as new insertions and deletions from the Array needs many data movements.

 

Although simple to manipulate, using arrays to store data may not be very efficient for applications that require frequent resizing, insertions, deletions and data updates. We note that Java API contains an ArrayList class that seems to provide flexible operations in all of the above cases. However, the internal representation of an ArrayList class requires some level of dynamic data management similar to a linked list data structure that we plan to discuss in this section. Unlike Java, many other practical languages such as C and C++ do not contain any facilities to similar to ArrayList in Java. Therefore it is necessary to understand data structures that allow us to manage applications that require resizing and frequent updates, inserts and deletes.

 

In this chapter we consider another data structure called Linked Lists that addresses some of the limitations of Arrays. However it should be noted that for some applications, Arrays are still the best data type to use. The decision to use an array or linked list to store data depends on the type of application. Now we begin by defining the concept of a linked list.

 

A linked list is a collection of objects linked together by references from an object to another object. By convention these objects are names as nodes. So the basic linked list, or commonly called singly linked list consists of nodes where each node contains one or more data fields AND a reference to the next node. The last node contains a null reference to indicate the end of the list. Unlike arrays where memory is allocated as a contiguous block of memory, the memory required for each node can be allocated as needed thereby providing a better way to manage free memory. The following diagram shows an example of a singly linked list.

 

     node              node             node

  _____________    ______________   ______________

  | data | ref |   | data | ref |   | data |      |

  |______|_____|-->|______|_____|-->|______|_null_|

     ^

     |

    head

 

The entry point into a linked list is always the head of the list. It should be noted that head is NOT a separate node, but a reference to the first Node in the list. If the list is empty then the head has the value null. Unlike Arrays, nodes cannot be accessed by an index. One must begin from the head and traverse the list to access the Nodes in the list. Insertions of new Nodes and deletion of existing nodes are fairly easy to handle (once you find the node) and will be discussed in the next lesson.

 

Types of Linked Lists

There are few different types of linked lists. A singly linked list as described above provides access to the list from the head node. Traversal is allowed only one way and there is no going back. The end of the list is indicated by a null reference. Here is an example of a singly linked list.

     12
 

     34
 

     56
 
 


                                                                                                                   null

 

                    Head

 


A doubly linked list is a list that has two references from each node, one to the next node and another to the previous node. Doubly linked lists also starts from head node, but provide access both ways. The flexibility of a doubly linked list is that one can traverse forward or backward from any node. A doubly linked list may be suitable for applications that require frequent updates to nodes that are in a close range. Here is an example of a

doubly linked list.

 

 


null                                                                                                                null

 

 

 

A multilinked list is a more general linked list with multiple links from nodes. For examples, suppose we need to maintain a list in two orders, age and name. We can define a Node that has two references, age pointer and a name pointer. Then it is possible to maintain one list, where if we follow the name pointer we can traverse the list in alphabetical order and if we traverse the age pointer, we can traverse the list by age.  This type of node organization may be useful for maintaining a customer list in a bank where same list can be traversed in any order (name, age, or any other criteria) based on the need. Here is an example of a multilinked list.

 

 

 

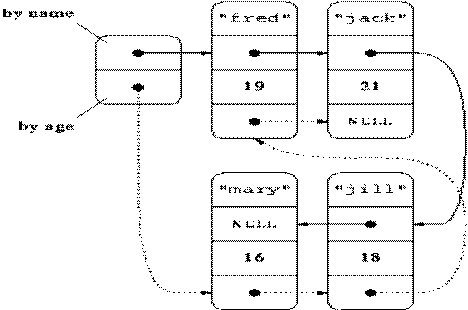
The above list shows how two pointers are maintained to follow the list in either age order or name order.  A more complex multilinked list can be used to store a “sparse” matrix as follow.

 

 

 

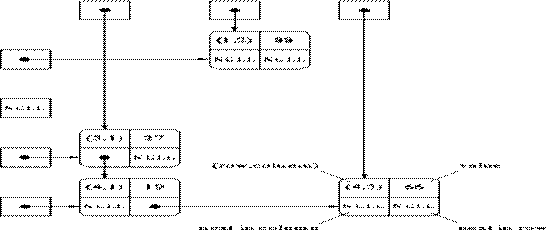
Another important type of a linked list is called a circular linked list where last node of the list points back to the first node (or the head) of the list. Here is an example of a circular singly linked list.                                      

 

 


                                                                    

 

 

 

 

 

 

 

 

 

 


Designing the Node Class

Each of the linked list structures defined above requires a node. The type of data stored in the node and number of links in the node defends on the type of linked list we need. Let us design the Node class to handle a singly linked list. A node is called a self-referential object, since it contains an instance variable that refers to an object of the same class.  For example, we may define a Node class as follows.

 

Class Node {

     public Comparable data;

     public Node next;

    // other methods    

}

 

The node class can use any comparable data type (that is any class that has implemented the Comparable interface). For example String and Integer are classes that already have the Comparable interface implemented. But if you define your own node data type, you can also implement the compareTo method to make sure those types can also be used in the Node class.

We can define three Node class constructors, one default, one that creates a Node object from data only and another that creates a data object from both Data and a link to another node. For example, a default constructor may work like this.

Node N = new Node();

Using a second constructor that takes an initial String as input, we can define a new Node as follows.

Node P = new Node("Pittsburgh");

The above statement allocates storage for an object referenced by P. The node P stores the string "Pittsburgh" and null reference. The statement

Node Q = new Node("Seattle", P);

Uses the third constructor and allocates storage for an object referenced by Q which stores the string "Seattle" and the address of node P, thereby connecting node P to node Q.

 

  _________________     ___________________

  | Seattle |     |    | Pittsburgh |      |

  |         |  o--|--->|            | null |

  -----------------    ---------------------

     ^                        ^

     |                        |

     Q                        P

 

These two statements can be written as one

Node Q = new Node("Seattle", new Node("Pittsburgh"));


·  Exercise.

Assume the following list

  ______________    _____________    _____________

  | "1" | next |   | "2" | next |   | "3" | null |

  |_____|______|-->|_____|______|-->|_____|______|

     ^

     |

     P

and explain the effect of each fragment below. The list is restored to its initial state before each line executes (assume that the Node class has all public fields).

1.      1.      p = p.next;

2.      2.      p.next = p.next.next;

3.      3.      p.data = p.next.data;

4.      4.      p.next.next.data = p.data;

 

Lvalue and Rvalue:

To be able to successfully manipulate with assignments and references, you need to understand a difference between left and right values. When we declare a variable

int i;

we inform the compiler of two things, the name of the variable and the type of the variable. On seeing the "int" part of this statement the compiler

- sets aside 4 bytes of memory to hold the value of the integer.
- sets up a symbol table, which contains the symbol i and the address of those 4 bytes.

Thus, if later on we write:

i = 2;

the value 2 will be placed in that memory location reserved for the storage of the value of i.
Now we see that two "values" associated with the object i:

rvalue - the integer (which is 2) stored there
lvalue - the address of i.

Consider the following example

int a, b;

a = 5;

b = a;

In the second line the compiler interprets a as the address (lvalue) of the variable a. In the next line - as the value (rvalue) of the variable a, stored at the memory location set aside during declaration. So each variable has actually two values

 

address or reference or LVALUE    AND     stored value or RVALUE

Now we apply this knowledge to

p.next = p.next.next;

The reference in the left hand side p.next. is a reference stored in the first node. According to the above argumentation, we take the lvalue of this reference. The reference in the right hand side p.next.next is a reference stored in the second node, which points to the third node. According to the above argumentation, we take the rvalue of it, which is the third node.

 

Therefore in order to manipulate linked lists using their references, we need to understand the differences between lvalue and rvalue of an identifier. In the next lesson we will discuss in detail how this is done as we try to implement linked lists operations.