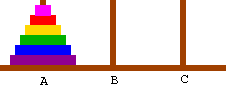
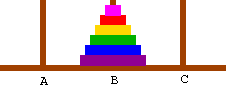
Up: Recursion. Prev: Recursion. Next: Program trace.

Writing a Towers of Hanoi program

Using recursion often involves a key insight that makes everything simpler. Often the insight is determining what data exactly we are recursing on - we ask, what is the essential feature of the problem that should change as we call ourselves? In the case of isAJew, the feature is the person in question: At the top level, we are asking about a person; a level deeper, we ask about the person's mother; in the next level, the grandmother; and so on.

In our Towers of Hanoi solution, we recurse on the largest disk to be moved. That is, we will write a recursive function that takes as a parameter the disk that is the largest disk in the tower we want to move. Our function will also take three parameters indicating from which peg the tower should be moved (source), to which peg it should go (dest), and the other peg, which we can use temporarily to make this happen (spare).

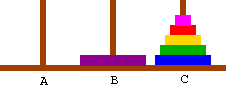
At the top level, we will want to move the entire tower, so we want to move disks 5 and smaller from peg A to peg B. We can break this into three basic steps.

  1. Move disks 4 and smaller from peg A (source) to peg C (spare), using peg B (dest) as a spare. How do we do this? By recursively using the same procedure. After finishing this, we'll have all the disks smaller than disk 4 on peg C. (Bear with me if this doesn't make sense for the moment - we'll do an example soon.)
  2. Now, with all the smaller disks on the spare peg, we can move disk 5 from peg A (source) to peg B (dest).
  3. Finally, we want disks 4 and smaller moved from peg C (spare) to peg B (dest). We do this recursively using the same procedure again. After we finish, we'll have disks 5 and smaller all on dest.

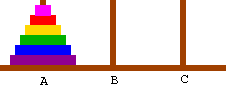
In pseudocode, this looks like the following. At the top level, we'll call MoveTower with disk=5, source=A, dest=B, and spare=C. 

FUNCTION MoveTower(disk, source, dest, spare):
IF disk == 0, THEN:
    move disk from source to dest
ELSE:
    MoveTower(disk - 1, source, spare, dest)   // Step 1 above
    move disk from source to dest              // Step 2 above
    MoveTower(disk - 1, spare, dest, source)   // Step 3 above
END IF

Note that the pseudocode adds a base case: When disk is 0, the smallest disk. In this case we don't need to worry about smaller disks, so we can just move the disk directly. In the other cases, we follow the three-step recursive procedure we already described for disk 5.

If this doesn't make sense to you, maybe an example run will help. Even if it does make sense, run through the example to make sure you understand. Understanding the concept of recursion is important to understanding the rest of the course.

Next: Program trace.