SD/FAST and MATLAB:
Simple Double Inverted Pendulum
Benjamin Stephens, Robotics Institute 2007
In this example, we will construct an SD/FAST model of a planar double inverted pendulum. A simulation will be created in C and run within MATLAB. The advantage of this approach is that data is passed very easily between the simulation and the MATLAB workspace for analysis. Also the SD/FAST simulation will be much faster than one written as a MATLAB function.
Create the Description File
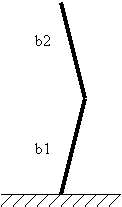
Below is a description file for a planar double inverted pendulum, like the one shown below. The pendulum has links of length 1 and mass 1.
 gravity = 0 -9.81 0
gravity = 0 -9.81 0
body = b1 inb = $ground joint = pin
mass
= 1
inertia
= 1 1 1?
bodytojoint = 0 -0.5 0
pin
= 0 0 1
body = b2 inb = b1 joint = pin
mass
= 1
inertia
= 1 1 1?
bodytojoint = 0 -0.5 0
inbtojoint = 0 0.5 0
pin
= 0 0 1
Here is the file: atest.sd
Compile the Code
SD/FAST:
> sdfast –lc –ge -n atest.sd (→ atest_dyn.c, atest_sar.c, sdlib.c, atest_info)
VC++:
> cl /c atest_dyn.c atest_sar.c sdlib.c (→ atest_dyn.obj, atest_sar.obj, sblib.obj)
The atest_info file looks like:
SD/FAST Information File: atest.sd
Generated 6-Mar-2007 10:25:40 by SD/FAST, Order(N)
formulation
ROADMAP (atest.sd)
Bodies Inb
No
Name body Joint type Coords q
--- --------- ---- ----------- ----------------
-1 $ground
0 b1 -1 Pin 0
1 b2 0 Pin 1
STATE INDEX TO JOINT/AXIS MAP (atest.sd)
Index
q|u
Joint Axis Joint type
Axis type Joint Name
----- -----
---- ----------- ----------
----------
0|2 0
0
Pin rotate
1|3 1
0 Pin rotate
SYSTEM PARAMETERS (atest.sd)
Parameter Value
Description
nbod 2
no. bodies (also, no. of tree joints)
njnt 2
total number of joints (tree+loop)
ndof 2
no. degrees of freedom allowed by tree joints
nloop 0
no. loop joints
nldof 0
no. degrees of freedom allowed by loop joints
nq 2
no. position coordinates in state (tree joints)
nu 2
no. rate coordinates in state (tree joints)
nlq 0
no. position coordinates describing loop joints
nlu 0
no. rate coordinates describing loop joints
nc 0
total no. constraints defined
nlc 0
no. loop joint constraints
npresc 0
no. prescribed motion constraints
nuserc 0
no. user constraints
Create a Mex File
The following c-file serves as a wrapper function between an sdfast simulation and MATLAB. The inputs are the initial state, state0, the desired state, state_des, an LQR gains matrix, K, and the total simulation time, endtime. The outputs are the time, times_out, the states, states_out, and the controls, torques_out.
#include "mex.h"
# define NQ 2
// number
of state position variables
# define NU 2
// number
of state velocity variables
# define NA 2
// number
of actuators
double torque[NA]={0};
void cpyvecd(double *oldvec, double *newvec, int length){
int i;
for(i=0;i<length;i++) newvec[i]=oldvec[i];
}
void mexFunction(int nlhs, mxArray
*plhs[], int nrhs, const mxArray *prhs[])
{
double *state0,*state_des,*K,*states_out,*time_out,*torques_out;
double state[NQ+NU], dstate[NQ+NU], time=0.0, endtime;
int flag=1, err, errest, LOCKQ[NU]={0}, LOCKU[NU]={0}, fcnt,
N;
int i,j,k;
int mrows, ncols;
// ASSIGN
INPUTS TO VARIABLES
state0 = mxGetPr(prhs[0]);
state_des=
mxGetPr(prhs[1]);
K = mxGetPr(prhs[2]);
endtime = mxGetScalar(prhs[3]);
// COPY
THE
cpyvecd(state0,&state[0],NQ+NU);
// DO SOME
CHECKS
mrows = mxGetM(prhs[2]);
ncols = mxGetN(prhs[2]);
if (!(mrows == (NQ+NU) && ncols
== NA)) {
mexErrMsgTxt("K matrix
must be transposed");
}
N=(int)(endtime/1e-3)+1;
// RESERVE
MEMORY FOR THE OUTPUTS
plhs[0] = mxCreateDoubleMatrix(1,N,mxREAL);
plhs[1] = mxCreateDoubleMatrix(NQ+NU,N,mxREAL);
plhs[2] = mxCreateDoubleMatrix(NA,N,mxREAL);
// CREATE
POINTER TO THE OUTPUTS
time_out
= (double *)mxGetPr(plhs[0]);
states_out
= (double *)mxGetPr(plhs[1]);
torques_out
=(double *)mxGetPr(plhs[2]);
//
INITIALIZE SDFAST
sdinit();
//
ASSEMBLE
sdassemble(time,&state[0],LOCKQ,1e-5,1000,&fcnt,&err);
if (err) mexPrintf("assmble error: %i\n",err);
// SAVE
cpyvecd(&time,&time_out[0],1);
cpyvecd(&state[0],&states_out[0],NQ+NU);
cpyvecd(&torque[0],&torques_out[0],NA);
// LOOP
UNTIL endtime
for(i=1;i<N;i++){
//
CALCULATE LQR TORQUE
for(k=0;k<NA;k++){
torque[k]=0.0;
for(j=0;j<NQ+NU;j++){
torque[k]-=K[k*(NQ+NU)+j]*(state[j]-state_des[j]);
}
}
//
INTEGRATE ONE TIMESTEP
sdfmotion(&time,&state[0],&dstate[0],1e-3,1e-3,&flag,&errest,&err);
if (err) mexPrintf("motion
error: %i at time: %6.3f\n",err,time);
//
ASSEMBLE THE SYSTEM
sdassemble(time,&state[0],LOCKQ,1e-5,1000,&fcnt,&err);
if (err) mexPrintf("assmble error: %i\n",err);
// SAVE
THE OUTPUT
cpyvecd(&time,&time_out[i],1);
cpyvecd(&state[0],&states_out[i*(NQ+NU)],NQ+NU);
cpyvecd(&torque[0],&torques_out[i*NA],NA);
}
}
void sdumotion(double T, double*Q, double*U){}
// sduforce(t,q,u) applies a user-defined
force
void sduforce(double T, double*Q, double*U){
int i;
// apply
torques to each joint
for(i=0;i<NA;i++) sdhinget(i,0,torque[i]);
}
Get this file here: mexSim.c
Compile the mex Program
>> mex mexSim.c atest_dyn.obj atest_sar.obj sdlib.obj chktk.obj (→ mexSim.mexw32)
Create a MATLAB Script to Run Simulation
The pendulum above can be described by a linearized discrete time state-space model Xi+1=AXi+BUi, where
 and
and
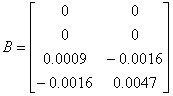
Using the DLQR() function in MATLAB, we can get a K gain matrix and use it in the script below:
K = [39.7840 10.6327 15.9696
5.0094
5.9724 8.9139
3.1899 3.0430];
[t,q,u] = mexSim([-0.1;0.1;0;0],[0;0;0;0],K',3);
subplot(2,1,1)
plot(t,q)
ylabel('angles (rad), velocities (rad/s)');
legend('q_0','q_1','q_2','q_3');
subplot(2,1,2);
plot(t,u);
xlabel('time(s)');
ylabel('torques (rad/s)');
legend('\tau_0','\tau_1');
This script produces the figure below:
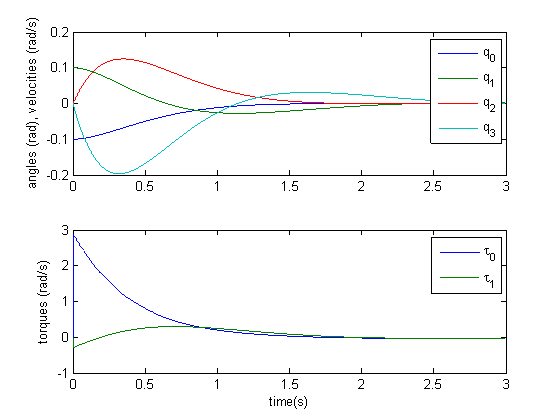
This code can be found here: runme.m