Interesting Map Problems

Don Knuth has written Volume 4 of the Art of Computer Programming. One of the chapters is on Binary Decision Diagrams and their applications, a subject that I find very interesting. Knuth shows that a variety of interesting graph problems can be encoded as Boolean formulas, and the derived BDD represents all possible solutions to the problem. Often there is some sort of optimization criterion, and it is fairly easy to extract the “best” solution from the BDD by a simple dynamic programming algorithm.

Here we show a few examples, using the graph representing the 48 contiguous states, with a node for each state, and an edge between two states if they share a border. For each of the maps, if you click on the image you will reach the source document in SVG format. Here is the graph, locating the nodes at the capitals of the states:

Capital Tours

Suppose you want to visit the 48 state capital with the requirement that you only pass through each state once. (In other words, you want to find a Hamiltonian path in the graph.) As you can see from the above map, if you follow the most direct route between state capitals, you will often pass through another state, or in the case of going from Lansing, Michigan to Madison, Wisconsin, you will drive across Lake Michigan. Instead, you should take the shortest driving route that stays within the two states for each leg of the journey. Let us call such a route a Capital Tour. Here is a diagram of the allowable routes between the states:

Based on a simple analysis, plus Knuth's efforts, we can say the following:

All tours must start or end in Maine, since Maine has only a single neighbor. We will use Maine as the starting point.
All tours must end beyond New York, since it is an articulation point.
There are 68,656,026 different capital tours overall.

Here is the shortest capital tour, totalling 11,698 miles:

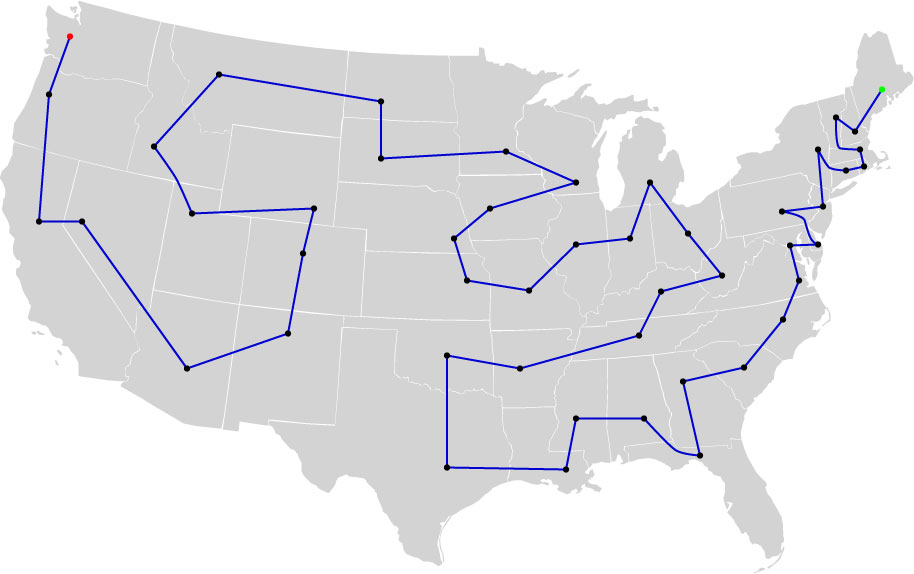
Here is the longest capital tour, totalling 18,040 miles:

Graph Coloring

Another interesting class of problems involves coloring the map. The rule is that no two adjacent states can have the same color. The famous Four Color Theorem states that any planar graph can be colored with at most four colors.

Since a BDD encodes all possible solutions to a Boolean formula, we can easily compute how many solutions there are. For graph coloring, we adjust our counts to eliminate symmetries due to the arbitrary assignment of color values (4! symmetric cases for 4-coloring).

For coloring the contiguous 48 states, there are 533,816,322,048 possible colorings. (This is 1/2 the number reported by Knuth, since his map includes Washington, DC as a 49th “state,” and it can be assigned either of the two colors not used for Maryland and Virginia.) Here are some interesting examples of special colorings:

A balanced coloring, in which each color is used for exactly 12 states. There are 12,554,677,864 such colorings, which is a surprisingly high 2.4% of all possible colorings.
An unbalanced coloring, in which one of the colors (green) is used as little as possible (2 states). There are just 288 ways to color the map such that one color gets used just twice.
An unbalanced coloring, in which one of the colors (yellow) is used as much as possible (18 states). There are 71,002,368 ways to color the map such that one color gets used 18 times.
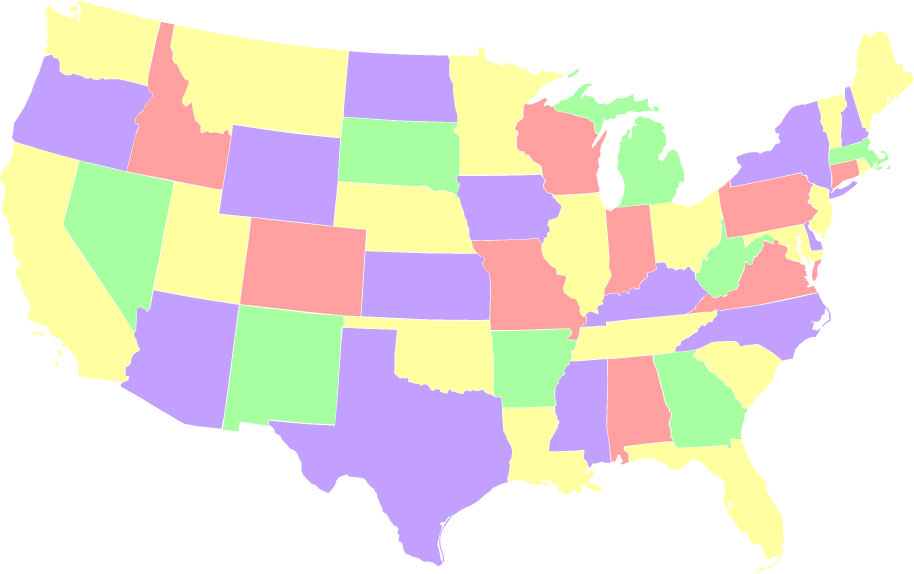
Combining both. Colorings using the colors 2, 13, 15, and 18 times. This sequence 1) from left to right, uses each color in succession for the fewest possible number of times, and 2) from right to left, uses each color in succession for the most possible number of times. There are 24 such solutions.

From the perspective of graph coloring programs, the map of the US 48 states is fairly simple. For a more challenging map, see the web page on the McGregor Graph.

Randal E. Bryant

Last modified: Tue Jan 19 07:48:18 EST 2010