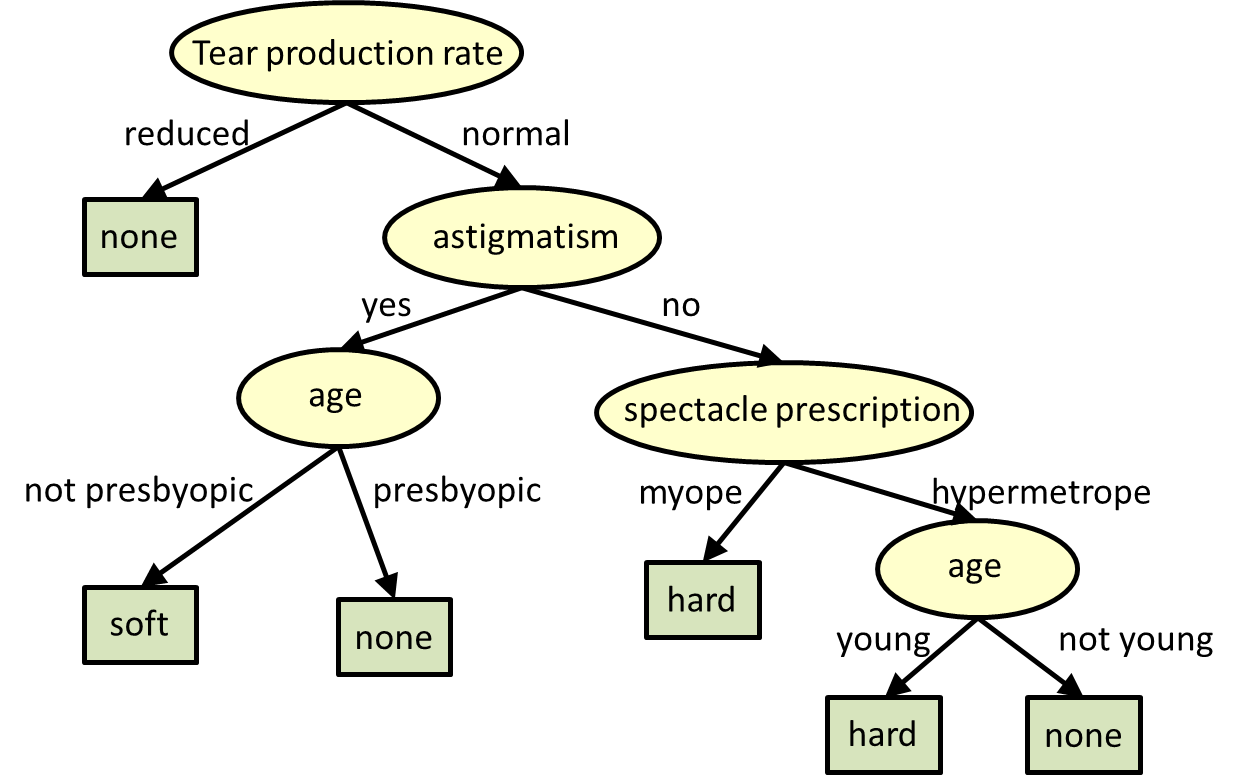
Caption: Decision tree to determine type of contact lens to be worn by a person. The known attributes of the person are tear production rate, whether he/she has astigmatism, their age (categorized into two values) and their spectacle prescription.
Key concepts:
Decision trees are tree-structured models for classification and regression.
The figure below shows an example of a decision tree to determine what kind of contact lens a person may wear. The choices (classes) are none, soft and hard. The attributes that we can obtain from the person are their tear production rate (reduced or normal), whether they have astigmatism (yes/no), their age category (presbyopic or not, young or not), their spectacle prescription (myopia or hypermetropia).

Caption: Decision tree to determine type of contact lens to be worn by a person. The known attributes of the person are tear production rate, whether he/she has astigmatism, their age (categorized into two values) and their spectacle prescription.
Decision trees can be learned from training data. Training data will typically comprise many instances of the following kind:
| Instance 1 | attribute1 | attribute2 | ... | attributeK | class |
| Instance 2 | attribute1 | attribute2 | ... | attributeK | class |
The decision tree learning algorithm recursively learns the tree as follows:
The following pseudo code describes the procedure. The pseudocode is a bit more detailed than your usual pseudo code, and doesn't follow any known standard :-)
In the pseudocode class variables are prefixed by “@” to distinguish them from locla varibles.
#------- Some "Helper" functions ---------------
# Segregating out instances that take a particular value
# attributearray is an N x 1 array.
def segregate(attributearray, value):
outlist = []
for i = 1 to length(attributearray):
if (attributearray[i] == value):
outlist = [outlist, i] # Append "i" to outlist
return outlist
# Assuming labels take values 1..M.
def computeEntropy(labels):
entropy = 0
for i = 1 to M:
probability_i = length(segregate(labels, i)) / length(labels)
entropy -= probability_i * log(probability_i)
return entropy
# Find most frequent value. Assuming labels take values 1..M
def mostFrequentlyOccurringValue(labels):
bestCount = -inf
bestId = none
for i = 1 to M:
count_i = length(segregate(label,i))
if (count_i > bestCount):
bestCount = count_i
bestId = i
return bestId
#-------- The Dtree code ------------
#Here "attributes" is an Num-instance x Num-attributes matrix. Each row is
#one training instance.
#"labels" is a Num-instance x 1 array of class labels for the training instances
# Note, we're storing a number of seemingly unnecessary variables, but
# we'll use them later for counting and pruning
class dtree:
float @nodeGainRatio
float @nodeInformationGain
boolean @isLeaf
integer @majorityClass
integer @bestAttribute
dtree[] @children
dtree @parent
init(attributes, labels):
@parent = null
buildTree (attributes, labels, self)
buildTree (attributes, labels, self):
numInstances = length(labels)
nodeInformation = numInstances * computeEntropy(labels)
@majorityClass = mostFrequentlyOccurringValue(labels)
if (nodeinformation == 0): # This is a "pure" node
@isLeaf = True
return
# First find the best attribute for this node
bestAttribute = none
bestInformationGain = -inf
bestGainRatio = -inf
for each attribute X:
conditionalInfo = 0
attributeEntropy = 0
for each attributevalue Y:
ids = segregate(attributes[][X], Y) # get ids of all instances
# for which attribute X == Y
attributeCount[Y] = length(ids)
conditionalInfo += attributeCount[Y] * computeEntropy(labels(ids));
attributeInformationGain = nodeInformation - conditionalInfo
gainRatio = attributeInformationGain / computeEntropy(attributeCount)
if (gainRatio > bestGainRatio):
bestInformationGain = attributeInformationGain
bestGainRatio = gainRatio
bestAttribute = X
#If no attribute provides andy gain, this node cannot be split further
if (bestGainRatio == 0):
@isLeaf = True
return
# Otherwise split by the best attribute
@bestAttribute = bestAttribute
@nodeGainRatio = bestGainRatio
@nodeInformationGain = bestInformationGain
for each attributevalue Y:
ids = segregate(attributes[][bestAttribute], Y)
@children[Y] = dtree(attributes[ids], labels[ids])
@children[Y].@parent = self
return
Once a decision tree is learned, it can be used to evaluate new instances to determine their class. The instance is passed down the tree, from the root, until it arrives at a leaf. The class assigned to the instance is the class for the leaf.
This procedure is explained by the following pseudocode.
class dtree:
[All the stuff from before here]
def evaluate(testAttributes):
if (@isLeaf):
return @majorityClass
else
return @children[testAttributes[@bestAttribute]].evaluate(testAttributes)
Decision trees that are trained on any training data run the risk of overfitting the training data.
What we mean by this is that eventually each leaf will reperesent a very specific set of attribute combinations that are seen in the training data, and the tree will consequently not be able to classify attribute value combinations that are not seen in the training data.
In order to prevent this from happening, we must prune the decision tree.
By pruning we mean that the lower ends (the leaves) of the tree are “snipped” until the tree is much smaller. The figure below shows an example of a full tree, and the same tree after it has been pruned to have only 4 leaves.
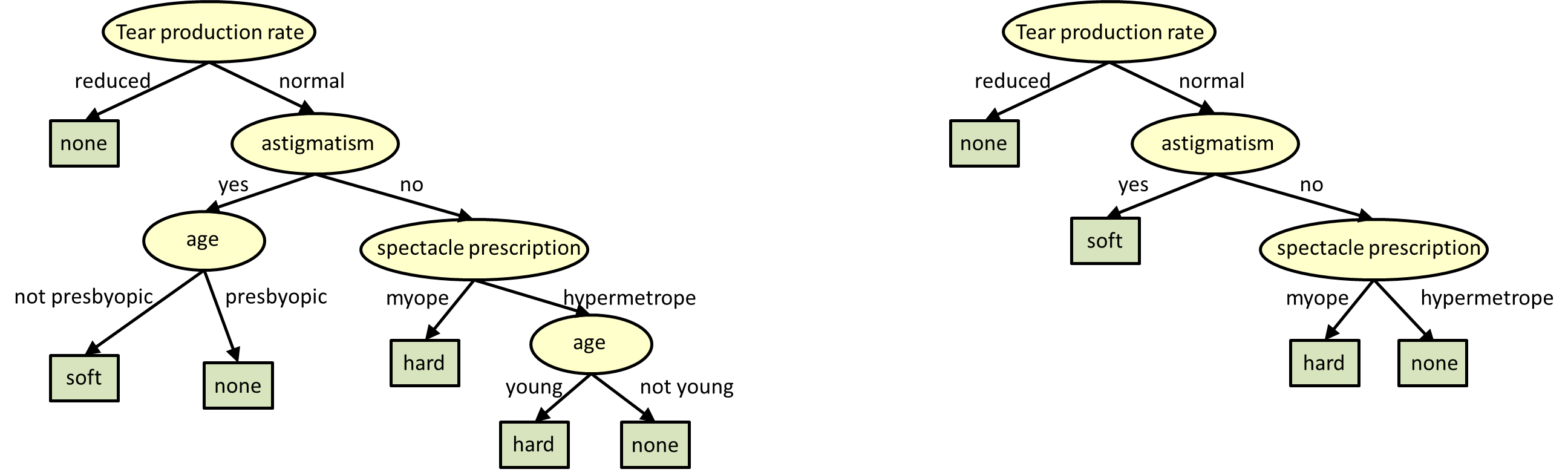
Caption: The figure to the right is a pruned version of the decision tree to the left.
Pruning can be performed in many ways. Here are two.
The process of IG-based pruning requires us to identify “twigs”, nodes whose children are all leaves. “Pruning” a twig removes all of the leaves which are the children of the twig, and makes the twig a leaf. The figure below illustrates this.

Caption: Pruning the encircled twig in the left figure results in the tree to the right. The twig now becomes a leaf.
The algorithm for pruning is as follows:
The pseudocode for this pruning algorithm is below.
# Count leaves in a tree
def countLeaves(decisiontree):
if decisiontree.isLeaf:
return 1
else
n = 0
for each child in decisiontree.children:
n += countLeaves(child)
return n
# Check if a node is a twig
def isTwig(decisionTree)
for each child in decisiontree.children:
if not child.isLeaf:
return False
return True
# Make a heap of twigs. The default heap is empty
def collectTwigs(decisionTree, heap=[])
if isTwig(decisionTree):
heappush(heap,(decisionTree.@nodeInformationGain, decisionTree))
else
for each child in decisiontree.children:
collectTwigs(child,heap)
return heap
# Prune a tree to have nLeaves leaves
# Assuming heappop pops smallest value
def prune(dTree, nLeaves):
totalLeaves = countLeaves(dTtree)
twigHeap = collectTwigs(dTree)
while totalLeaves > nLeaves:
twig = heappop(twigHeap)
totalLeaves -= (length(twig.@children) - 1) #Trimming the twig removes
#numChildren leaves, but adds
#the twig itself as a leaf
twig.@chidren = null # Kill the chilren
twig.@isLeaf = True
twig.@nodeInformationGain = 0
# Check if the parent is a twig and, if so, put it in the heap
parent = twig.@parent
if isTwig(parent):
heappush(twigHeap,(parent.@nodeInformationGain, parent))
return
An alternate approach is to prune the tree to maximize classification performance on a validation set (a data set with known labels, which was not used to train the tree).
We pass the validation data down the tree. At each node, we record the total number of instances and the number of misclassifications, if that node were actually a leaf. We do this at all nodes and leaves.
Subsequently, we prune all twigs where pruning results in the smallest overall increase in classification error.
The overall algorithm for pruning is as follows:
Stage 1:
The pseudocode for this pruning algorithm is below.
# First pass : evaluate validation data and note the classification at each node
# Assuming that "valData" includes "attributes" and "labels"
# First create an empty list of error counts at nodes
def createNodeList(dTree, nodeError=[]):
nodeError[dTree] = 0
for child in dTree.@children
createNodeList(dTree, nodeError)
return nodeError
# Pass a single instance down the tree and note node errors
def classifyValidationDataInstance(dTree, validationDataInstance, nodeError):
if (dTree.@majorityClass != validationDataInstance.label):
nodeError[dTree] += 1
if (not @isLeaf):
childNode = dTree.@children[testAttributes[@bestAttribute]]
classifyValidationDataInstance(childNode, testAttributes, nodeError)
return
# Count total node errors for validation data
def classifyValidationData(dTree, validationData):
nodeErrorCounts = createNodeList(dTree)
for instance in validationData:
classifyValidationDataInstance(child, instance, nodeErrorCounts)
return nodeErrorCounts
# Second pass: Create a heap with twigs using nodeErrorCounts
def collectTwigsByErrorCount(decisionTree, nodeErrorCounts, heap=[])
if isTwig(decisionTree):
# Count how much the error would increase if the twig were trimmed
twigErrorIncrease = nodeErrorCounts[decisionTree]
for child in decisionTree.@children
twigErrorIncrease -= nodeErrorCounts[child]
heappush(heap,(twigErrorIncrease, decisionTree))
else
for each child in decisiontree.children:
collectTwigsByErrorCount(child, nodeErrorCounts, heap)
return heap
# Third pass: Prune a tree to have nLeaves leaves
# Assuming heappop pops smallest value
def pruneByClassificationError(dTree, validationData, nLeaves):
# First obtain error counts for validation data
nodeErrorCounts = classifyValidationData(dTree, validationData)
# Get Twig Heap
twigHeap = collectTwigsByErrorCount(dTree, nodeErrorCounts)
totalLeaves = countLeaves(dTtree)
while totalLeaves > nLeaves:
twig = heappop(twigHeap)
totalLeaves -= (length(twig.@children) - 1) #Trimming the twig removes
#numChildren leaves, but adds
#the twig itself as a leaf
twig.@chidren = null # Kill the chilren
twig.@isLeaf = True
twig.@nodeInformationGain = 0
# Check if the parent is a twig and, if so, put it in the heap
parent = twig.@parent
if isTwig(parent):
twigErrorIncrease = nodeErrorCounts[parent]
for child in parent.@children
twigErrorIncrease -= nodeErrorCounts[child]
heappush(twigHeap,(twigErrorIncrease, parent))
return
Pruning may also use other criteria, e.g. minimizing computational complexity, or using other techniques, e.g. randomized pruning of entire subtrees.