Investigating The Utility of MMX/SSE Instruction Sets Now And In The Future

CS 15-740 Computer Architecture Final Project Report

Computer Science Department

Carnegie Mellon University

Jernej Barbic

Brian Potetz

Matt Rosencrantz

Abstract:

In this report we examine several multimedia applications with and without MMX/SSE enhancements and examine the impact on execution time and cache performance of these enhancements. We implement several versions of the programs to isolate their memory and processing requirements.One criticism of SIMD technology is that it may be doomed to obsolesence as processors gain speed with respect to memory. We discover that the multimedia applications we looked at are not memory bound. Enhancing applications with MMX does make them more memory bound, but not so much as to nullify the gain given by the enhancement. We show that prefetching instructions can be used to hide memory latency, and that MMX style enhancement will still be useful as long as the latency is predictable, the memory bandwidth scales sufficiently, and the total runtime of the program is large compared to the latency of memory.

1 Introduction and Previous Work

Our first goal is to test the ability of MMX and SSE to improve the performance of multimedia applications. In this paper, we compare enhanced and unenhanced versions of a wide variety of applications, representative of important multimedia workloads both today and in the future. There has been some work in this area, but there are still many unexplored avenues. In particular, Bhargava et. al investigated performance enhancements gained by MMX instructions on a suite of multimedia applications [2], but relied on the use of Intel MMX enhanced image processing libraries to gain performance. This introduces waste due to operand arrangement and function call overhead. Worse still, the libraries implement generalized algorithms that cannot take advantage of simplifications allowed when targeting a specific application. For example, JPEG only requires 8x8 inverse discrete cosine transform (IDCT) operations and a general implementation of IDCT would not be able to take advantage of that fact. This may have been why they observed a negative performance gain in their JPEG implementation. Additionally, SSE and prefetching were not explored.

We are also interested in investigating the continued utility of these multimedia instruction sets. One criticism of SIMD instructions has been that processor speeds have been increasing faster than memory access times, and that multimedia workloads are known to process large quantities of data. It would therefore seem possible that the utility of SIMD may be decreasing as multimedia applications become more memory-bound, and that eventually it may no longer be worth supporting. In this paper we use a variety of methods to test the veracity of this claim.

Slingerland et. al conducted a detailed analysis of the cache performance of multimedia applications and concluded that they actually exhibit lower instruction miss ratios and comparable data miss ratios when contrasted with other widely studied workloads [4]. In [6], the authors studied the effect of using Sun’s VIS instruction set. After adding VIS instructions, some applications that had been compute bound became memory bound. After inserting software prefetching, however, the applications became process bound again. One shortcoming of this experiment was that the simulator used the RSIM superscalar processor simulator. We seek to establish similar results on a real world processor that is in common use, instead of using a simulator for a non-existent CPU.

2 Methodology

All our results were collected on Pentium III 1GHz computers running Windows 2000 with 512MB or RAM, 512K L2 cache, and 16K instruction and data L1 caches. The cache line size is 32 bytes for both L2 and L1, and all caches are write-back.

2.1 No-Memory Mode

The first quantity we wish to measure is the amount of time wasted by programs due to cache misses. This statistic is somewhat difficult to obtain, however, because it is difficult to judge when an out-of-order superscalar processor is wasting time, and more difficult still to give a precise reason for the waste when it occurs. A crucial observation, however, is that a computer with an infinite pre-loaded cache would give us the performance of the program without any waste due to bad cache performance, and we would then be able to compute the wasted time by a simple subtraction. Unfortunately, it is not feasible to build such a device, and no simulator was available that we could alter to achieve this behavior. This same functionality can be simulated, though, by simply altering all loads and stores in the program to always read from a single small static buffer instead of traversing the enormous sea of data usually processed by the algorithm.

In general, this method of measurement is not practical. In particular, it cannot be performed if the flow control of a program is dependent on the data you are trying to isolate it from. Fortunately, there is a large class of multimedia applications whose control flow is independent of the data: decoding applications. Decoding applications often do not make decisions based on their data, they simply churn through it passing data from input through a series of steps to the output. The procedure applied is independent of the data, which means that it will take as long to process a simple repeating pattern of bytes as it would to process actual image data.

A final implementation detail that can arise when using this strategy is that artificial instruction dependencies can be introduced by altering the loads and stores, making the code run artificially slow. To avoid this problem, separate buffers can be used for reading and for writing, minimizing false dependencies and forcing all dependencies to be either read after read or write after write, which are more palatable than other dependency types in practice.

We implemented this modification on several applications of our multimedia suite and successfully used it to isolate the time wasted by bad cache performance from the time required to perform the processing alone. We call these modified versions no-memory mode versions. We made use of another simplifying idea: you need not implement no-memory mode everywhere, but only in "hot spots" that exhibit a large number of cache misses. In this way a large percentage of the cache misses in a program can be eliminated with relative ease.

2.2 No-Processor Mode

Using the no-memory mode versions of our applications, we are able to compute the portion of program execution spent processing data and differentiate this from time lost due to cache misses. However, we would like to make a further distinction. We would like to know the portion of the execution spent performing any memory access. In effect, the running time of a program can be visualized as a Venn diagram where the two circles are the time required for computation and the time required purely for memory operations. The overlap signifies the time that the CPU is able to schedule computation while a memory operation is being serviced.

We know the total time, and from our no-memory-mode, we know the time spent only processing. In order to determine the overlap time in the diagram, we need to measure the time required to execute just the memory operations of our program. To achieve this we created a special version where we essentially removed all the instructions that were not memory instructions, thereby making the program completely memory-bound. We call this modification no-processor mode.

Again, this technique is not universally applicable. The validity of this approach assumes that no prefetching is taking place in normal operation of the program. Furthermore, some amount of processing is clearly required to execute no-processor mode, including loop overhead and pointer arithmetic. We can only expect that the time required to execute these few processing instructions will be hidden by the memory access costs.

It should be noted here that these concepts are only approximations of the behavior of the processor during multimedia processing. Running the program in no-memory mode will change the burden somewhat on processor resources. If we are in no-memory mode then dependancies that might have worked themselves out durring a cache miss will now be seen by the processor, thus decreasing efficiency. If, however, we are not running no-memory mode the cache misses will cause long latency dependancies that will likely force many instructions to queue up, filling the reorder buffer. This will not be seen in no-memory mode. In any case the effects of these changes will be small as long as there are very few cache misses reletive to the dynamic instruction count. We feel that the no-memory mode abstraction provides an excellent way to gain insight into the relative extent to which a multimedia application is processor-bound or memory-bound.

2.3 Application Suite

2.3.1 JPEG

The first application that we study is the JPEG decoder algorithm. As mentioned above, the JPEG algorithm is important to study because it is a real-world multimedia application that is ubiquitous to a wide population of computer users, and yet previous attempts to improve its performance using MMX have failed [2]. Although JPEG decompression is not usually a noticably slow application, it is still important to improve its performance to help support multimedia applications that display large numbers of images concurrently with other processes, the ability to pan smoothly across large images, or real-time decompression of high-resolution MJPEG movies.

To investigate the utility of MMX for JPEG decompression, we chose to enhance the open-source JPEG library provided by the Independent JPEG Group (IJG). The advantage of selecting this library is that it is in wide use, and has been optimized for efficient JPEG decoding. This ensures that we have a realistic base to compare our MMX enhanced algorithm to. Using a profiler, we identified three processing-intensive “hot-spots” of the decoder: the inverse discrete cosine transform (IDCT), the color conversion routine, and the linear interpolation upsampling routine. We were able to find existing enhanced versions of two of these routines (the IDCT and the upsampler) as a part of an open-source project to implement a fast MJPEG encoder/player. We completed their implementation and then modified the code for no-memory and no-processing mode by hand in the hot-spots mentioned above. The results reported for the unenhanced version of JPEG are from the original C++ source compiled on Microsoft Visual C++ 6.0 with optimizations.

All tests of the JPEG decoder were run on a 10,000x10,000 pixel 24 bit color JPEG image. As a compressed image, this image consumes 13,302,614 bytes. The large size of the image was chosen to reduce the effect of overhead on program execution, to decrease the relative error introduced by event sampling in VTune, and to demonstrate the performance of JPEG decompression on high-resolution images, which is likely to become more important as consumer-level bandwidth and disk-capacity increases and large images become more commonplace.

2.3.2 Sobel Edge Detector

The next application in our test suite was a simple computer vision algorithm. Specifically, we chose a simple edge-detection algorithm, the Vertical Sobel convolution operator. This algorithm works by applying a small 3x3 convolution to the image. We selected this application for several reasons. First, to further understand how MMX will be useful both now and in the future, we specifically sought out algorithms that were pertinent to developing, up and coming applications of computing technology. Computer vision is an area that we expect to see growth in as processors become faster and more practical for demanding image understanding applications. Also, we may expect that in the future, computer vision may become a task that users will want to perform concurrently with other processing tasks. For instance, users may want to interact with a computer via face and gesture recognition software, without sacrificing a large portion of their processing capability.

Finally, and most importantly, we chose the Sobel operator because we wanted to analyze an algorithm that required a very small amount of processing per memory access. The Sobel convolution operator exemplifies this behavior. For each pixel of output (one byte each), the Sobel algorithm loads six neighboring pixels, performs three integer adds operations, three subtracts, a multiply and a shift. We can expect, therefore, that the Sobel convolution operator should be as close to memory-bound as one can find in a multimedia algorithm.

All versions of the Sobel operator were written from scratch, in either C++, Intel assembly, or MMX/SSE enhanced Intel assembly. The unenhanced version of the algorithm was originally written in C++, and compiled with an optimizing compiler (Microsoft Developer Studio 6.0). The C++ code was then assembled into Intel assembly, so that further modifications to the code could be made without worrying about complexities introduced by the optimizing compiler. Several attempts were made to modify the resulting assembly code to improve the unenhanced algorithm, but no performance boost was realized. This discredits the possibility that some of the gain from MMX was due to more careful fine-tuning at the assembly level. MMX and MMX/SSE versions of the algorithm were implemented directly in assembly. No-memory and No-processing modes for both the enhanced and unenhanced versions were also implemented directly in assembly. Because the algorithm uses only integer arithmetic, the SSE enhanced version differs from the MMX enhanced version only in its use of software prefetching.

All versions of the Sobel operator application were run a 10,000x10,000 pixel grayscale image. All results shown reflect the performance of the Sobel operator itself. They do not include the execution of decompressing the image or reading it from disk.

2.3.3 MP3 and MPEG Encoders

To study mp3 compression we used the Gogo No Coda mp3 compression utility. This utility converts wav files into mp3's. The reason for choosing this application is that it comes with a full source code and that it enables to turn on/off SSE or MMX features.

To study mpeg compression we used the Flask Video mpeg compressor which converts DVD uncompressed files (vob) into mpeg-2 format. We performed the tests on a 39.1 Mb vob file to convert it into a 5 Mb mpeg-2 file. Again, the MMX and non-MMX version produce two mpeg-2 file of essentially the same quality.

All tests were performed on a 20 Mb wav file taken from a musical CD. Resulting mp3 file size was 1.8 Mb. The mp3 files produced by MMX and non-MMX routines were identical, whereas the SSE-produced version had the same length as MMX and non-MMX version, but slightly different data with the same sound sampling frequency.

2.4 Using VTune

Intel's VTune is one of the standard performance analyzers for the x86 architectures. It uses Pentium on-chip performance-monitoring hardware counters that keep track of many processor-related events (see [1], Appendix A). For each event type, VTune can count the total number of events during an execution of a program and locate the spots in the program's source code where these events took place (with corresponding frequencies). We used VTune to gather statistics on the following event types:

· Clockticks

· Total instructions retired

· L1 cache line allocated

· L1 misses outstanding (roughly this equals the number of L1 cache misses times the average number of cycles to service the miss)

· L2 Cache Read Misses

· L2 Cache Write Misses

· L2 Cache Instruction Fetch Misses

· L2 Cache Request Misses (equals the sum of the previous three categories)

· L2 Cache Reads

· L2 Cache Writes

· L2 Cache Instruction Fetches

· L2 Cache Requests (equals the sum of the previous three categories)

VTune performs these measurements by sampling, which is inherently inaccurate. VTune implements a self-calibration mechanism which allows us to set the desired accuracy (in our case: 5%) of the results.

Additionally, VTune also permits to perform a dynamic analysis (simulation) of a portion of a code. The simulation takes a lot of time and is therefore useful mainly for short segments of code. We used dynamic analysis to better understand the program behavior at hot-spots.

3 Results

3.1 JPEG

Overall, the MMX enhanced version of JPEG achieved a speedup of 1.7x or 41.2%. In order to take a closer look at cache performance, we implemented a special no-memory-mode version of both the enhanced and unenhanced programs. In the unenhanced version, despite the fact that L1 weighted outstanding misses has dropped a precipitous 97%, the decompression time for the JPEG has decreased by only 0.5%, probably within the margin of error of our measurement. This is a clear demonstration that the program was wasting very little, if any, of its time on cache misses. In the enhanced version of the code, one might expect to encounter a much different situation since processing has been sped considerably, perhaps making memory more of a bottleneck. Again, however, the data show that a 97% decrease in L1 misses outstanding produces a paltry 4.3% performance improvement. This is strong evidence that the MMX version of the application, while more memory constrained than its unenhanced alternative, is still processor bound. To build some intuition for why so little time is wasted due to cache misses we can examine the number of L1 weighted outstanding misses. Assuming that all L1 misses were non-overlapping and that no useful computation could be done while any miss was outstanding we would have wasted only about 154 million instructions, which is only about 3.1% of the total cycles. Put another way, we can note that the total number of L2 request misses for our MMX enhanced program was approximately 2,387,000. Suppose each of these misses incurred a penalty of 100 cycles and that the processor was completely unable to hide any of it by batching requests or issuing other instructions. Even in these dire conditions only 238,700,000 cycles would be wasted, this number is a mere 4.8% of the nearly 5 billion cycles required to process the entire JPEG image. There simply is not very many cache misses relative to the amount of computation. Only about one in every thousand memory requests resulted in an L2 miss, which is only about one in every three thousand instructions.

Table 1: Overall JPEG Performance

Algorithm Version	Execution Time (cycles)
Unenhanced	10,628,268,688
Unenhanced, No-Memory Mode	10,573,118,081
MMX enhanced	4,922,172,952
MMX enhanced, No-Memory Mode	4,711,002,535

Table 2: L1 Cache Analysis

Algorithm Version	Cycles L1 Misses Outstanding	Total Cycles	Percent
Unenhanced Version	188,336,797	10,628,268,688	1.77%
MMX Version	154,240,083	4,922,172,952	3.13%

3.1.1 IDCT

In order to get a better insight into what makes the JPEG application perform so much faster when MMX enhanced, we will examine several "hotspot" functions. Perhaps the most important of these “hotspots” is the inverse discrete cosine transform function. This function represents 41.55% and 35.33% of the unenhanced and enhanced program execution times respectively. It is also the source of the greatest speed up, 2.0x or 50.0%. Looking at our special no-memory-mode versions of the MMX and unenhanced code performance increases of 10.2% and 2.8% respectively are observed. We can see here perhaps more clearly that the MMX enhanced code has more of a memory bottleneck than the unenhanced program, but neither is seriously constrained.

Table 3: IDCT Performance

Algorithm Version	Execution Time (cycles)
Unenhanced	5,725,448,342
Unenhanced, No-Memory Mode	5,566,746,670
MMX enhanced	1,739,003,704
MMX enhanced, No-Memory Mode	1,562,639,541

Figure 1: JPEG Hotspot Execution Time Breakdown

3.1.2 Upsampling

The fancy upsample routine is somewhat shorter and simpler than the IDCT and so we were able to implement the no-processor-mode. With this information we can construct the full Venn diagram.

We achieved a speedup of 3.29x in this function.

Table 4: Upsampling Performance

Algorithm Version	Execution Time (cycles)
Unenhanced	1,003,308,564
MMX enhanced	412,478,093
MMX enhanced, No-Memory Mode	362,747,195
MMX enhanced, No-Processing Mode	133,062,946

3.1.3 Color Conversion

The speed-up obtained for this JPEG hotspot was 2.14x. As shown in Figure 1, analysis of no-memory and no-processing modes show that the algorithm is almost entirely processor-bound. The relative number of L1 misses, shown in Table 6, supports this conclusion.

Table 5: Color Conversion Performance

Algorithm Version	Execution Time (cycles)
Color Conversion, Unenhanced	2,312,153,133
Color Conversion, MMX enhanced	1,080,249,951
Color Conversion, MMX enhanced, No-Memory Mode	952,208,118
Color Conversion, MMX enhanced, No-Processing Mode	304,961,077

Table 6: L1 Cache Performance

Algorithm Version	Cycles L1 Misses Outstanding	Total Cycles	Percent
Color Conversion, Unenhanced	74,471,228	2,312,153,133	1.43%
Color Conversion, MMX enhanced	69,925,288	1,080,249,951	3.05%
Upsample, Unenhanced	66,369,887	1,003,308,564	6.62%
Upsample, MMX enhanced	58,117,663	412,478,093	14.10%

3.2 Sobel Edge Detector

The most impressive speed-up we observed was in our simple computer vision algorithm. Using MMX alone, we obtained a speed-up of 2.50x. When the prefetching capabilities of SSE were added, the speed-up jumped to 4.19x. We can understand these results better by investigating the memory and processing requirements of our algorithm.

First, it is important to understand the effect of MMX on the inner loop of our kernel. As mentioned above, for each iteration of the inner loop, the unenhanced version of the algorithm performs six memory loads of one byte each, three integer adds, three subtracts, a multiply and a shift (plus a small amount of loop overhead and pointer arithmetic), and then stores one byte to memory. The MMX version of the algorithm performs two loads of eight bytes each, performs six packed adds, six packed subtracts, two packed multiplies, two packed shifts, and performs two stores of four bytes each. Therefore, the total number of processing calls have decreased by a factor of four, the total number of memory read instructions has decreased by a factor of 48, and the total number of memory write instructions has decreased by a factor of four.

We then ran our no-memory-mode and no-processing-mode versions of the algorithm and compared them with the originals. For the unenhanced algorithm, the no-processing mode algorithm took 56% as much time as the complete algorithm. The no-memory mode algorithm took 72% as much time as the complete algorithm. This suggests that both processing and memory access are critical to the execution of the algorithm, but the processing demands were slightly greater than the memory access demands.

Table 7: Sobel Edge Detector Performance

Algorithm Version	Execution Time (ticks)
Unenhanced	2781
Unenhanced, No-Memory Mode	2000
Unenhanced, No-Processing Mode	1552
MMX enhanced	1110
MMX enhanced, No-Memory Mode	630
MMX enhanced, No-Processing Mode	859
MMX/SSE enhanced (prefetching)	661
MMX/SSE enhanced, No-Memory Mode	630

For the MMX enhanced version of the algorithm, the no-processing mode algorithm took 77% as long as the complete enhanced algorithm, while the no-memory mode version took 57% as long. So we can see that adding MMX to the algorithm made the program more memory-bound, although both computation and memory are still very critical to algorithm.

From these results, we can also estimate that MMX increased the performance of the processing portion of the algorithm by a factor of 3.16, and it increased the performance of the memory portion of the algorithm by a factor of 1.82. The speed-up to the processing portion approached its theoretical maximum

Figure 2 Sobel Edge Detector Execution Breakdown

of 4x. The speed-up to the memory portion was most likely due to the great reduction of memory access instructions (the MMX version has only 2.08% as many load instruction as the unenhanced version).

Because our simple vision algorithm was not entirely processor-bound, it presents an excellent opportunity to explore the utility of the prefetch instructions provided by SSE. As MMX decreases the size of the processing portion of our execution time, the algorithm becomes more memory-bound. We want to investigate the ability of software prefetching to remedy this problem.

We implement a very simple form of prefetching here, prefetching only for image data in the inner loop of the algorithm. The number of iterations to prefetch data in advance is determined by increasing this number until no more reduction of cache misses can be obtained, and VTune dynamic analysis reports no data_pending cache misses.

After prefetching was added, the program ran in 60% of the time required for the MMX enhanced version. The no-memory-mode version (the same executable as the no-memory version for the MMX algorithm without prefetching) required a full 95% of this time to complete. This is to be expected, since the prefetching version of the algorithm cannot be expected to run faster than the processing portion of the non-prefetching MMX version, which took 57%. This self-consistency within the data lends credibility to its validity.

Table 8: Sobel Edge Detector L1 Cache Performance

Algorithm Version	Cycles L1 Misses Outstanding	Total Cycles	Percent
Unenhanced Version	350,577,036	2,648,201,359	13.24%
MMX Version	481,796,621	1,033,714,579	46.61%
MMX/SSE Version	40,326,338	612,531,161	6.58%

Unfortunately, it does not make sense to implement no-processing-mode for the prefetching MMX/SSE version of the algorithm. By removing the processing instructions from the inner loop, the loop will become memory-saturated, thereby altering the number of iterations in advance prefetches must be issued, and clogging the data bus with memory requests. So we cannot complete the Venn diagram for the prefetching algorithm. However, we can infer from the results above that the memory portion of the diagram must lie almost entirely within the processing portion of the diagram. This theory is born out by examining the number of cache misses in the prefetching version. By adding prefetching, the weighted number of cycles while an L1 cache miss was outstanding reduced from 481,796,621 to 40,326,338. This is a 12x reduction. This suggests that the memory portion of our diagram has not only moved inward to overlap the processing portion, but it has become significantly smaller.

3.3 MP3 & MPEG Compression

VTune Sampling shows a significant decrease in the total number of clockticks as MMX and SSE features are added. At the same time, the number of dynamic instructions issued decreases. SSE version took 7.3 seconds, MMX version took 11.2 seconds and non-MMX version took 12.4 seconds. Cache characteristics do not differ much between non-MMX, MMX and SSE versions. This is not surprising since all the three version operate on the same data in the same order. Results for mpeg are similar to those for mp3. The MMX version took 111 seconds and no-MMX version took 130 seconds. The following three diagrams summarize these results.

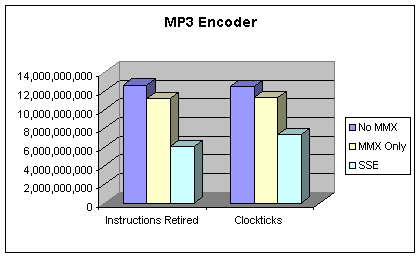
Figure 3: MP3 Compression Performance

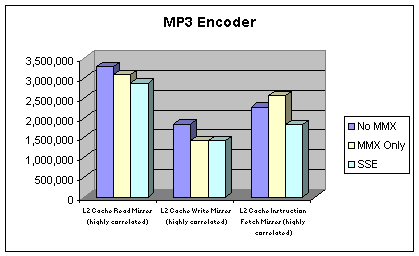
Figure 4: MP3 L2 Cache Performance

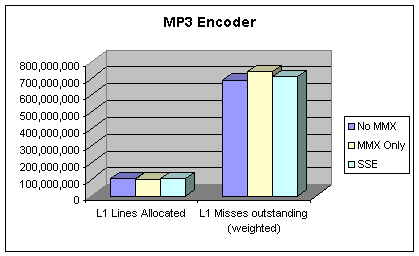
Figure 5: MP3 L1 Cache Performance

We couldn't use the no-memory mode techniques to analyze compression algorithms since the speed of compression (detecting motion vectors) depends much more on the input data than does decompression. We used the following technique, which gives us an upper bound on the relative number of cycles wasted due to cache misses. If this upper bound is very low, we can then argue that the program is not memory-bound. Every L2 cache miss takes approximately 100 cycle to serve. With VTune, we can determine the total number n of L2 cache request misses (data reads + data writes + instruction misses). Under the pessimistic assumption that the processor stalls while servicing a L2 cache miss (i.e. that there is no intersection of memory and processor mode), it follows that in the worst case 100n cycles are wasted waiting for data from memory. In reality, there is some overlap of memory and processor mode, so the number of wasted cycles will be much lower. With VTune, we can measure the total number of cycles issued in the program (processor frequency * total execution time) and we can therefore determine the ratio k:

In this equation, wasted cycles refers to the actual number of cycles the program execution is stalled due to memory latency. This corresponds to the memory-only part of the Venn diagram.

For the mp3 compression, the ratios k are (10%, 6.4%, 5.7%) for (SSE, MMX, non-MMX) respectively, and for mpeg compression they are (29.7%, 25.2%) for (MMX, non-MMX), respectively. Note that the ratios get higher as you add more and more efficient computation, i.e. as you add MMX and SSE instructions.

The ratios for mp3 are very small, which implies that mp3 compression algorithm is compute-bound and not memory-bound. Since the k ratio is only an upper bound on the relative number of cycles wasted, relatively high numbers for mpeg do not necessarily imply that mpeg computation is memory-bound. Actually, MMX version of mpeg experiences a 20% speedup over the non-MMX, supporting the argument that mpeg compression is not memory bound.

Introducing the two multimedia instruction sets has therefore decreased the compute time for mp3 and mpeg compression, but not to the extent that memory would become a bottleneck.

3.4 Unreal Tournament

Another important class of multimedia applications is computer games. In order to get some idea of the impact of MMX on video game performance we ran Unreal Tournament on the Utbench benchmark. We recorded frames per second values in MMX and no-MMX mode at 800X600 resolution with default quality settings. We observed significant frame rate increases in MMX mode.

Table 9: Unreal Tournament Frame Rates

	No-MMX	MMX
Min Frame Rate	11.81	15.97
Max Frame Rate	20.88	25.95
Average Frame Rate	17.08	20.39

4 Conclusions

Our first goal was to demonstrate performance gain using MMX and SSE. In every case we were able to derive some performance benefit from MMX optimization, often a quite large benefit. By avoiding the use of prefabricated MMX image processing libraries, we were able to achieve a sizable performance increase in the JPEG decoder, although previous work had been unable to do this. Our simple computer vision algorithm demonstrated a performance boost that approached the theoretical maximum for four-data-element SIMD. These results show that MMX technology is very useful today.

Our second goal was to test the claim that the utility of SIMD technology was doomed to obsolescence as processors gained in speed with respect to memory. The fact that significant performance increase was observed on MMX enhanced versions of our multimedia suite suggests that if this is true, this event is still a long ways away. Even in the case of the Sobel algorithm, which has very little computation per byte of input data, we saw a large improvement from using MMX. Enhancing applications with MMX does make them more memory bound, but there is enough processing to be done that even in this case there is a speed-up. However, we can see that as long CPU speed increases at a faster rate than memory speed this improvement will be decreasing.

Our results when using the SSE Prefetching instructions, though, show that there is a way to circumvent the problems caused by this widening gap. We can use prefetching instructions to hide memory latency as long as the latency is predictable, the working set of the algorithm is sufficiently small, the pattern of data access is predictable, the memory bandwidth scales sufficiently, and the total run-time of the program is large compared to the latency of memory. The latency of memory must be predictable so we can accurately determine how far in advance to prefetch data. Slingerland et. al showed that the working sets of multimedia applications are generally small (16K-32K) except in the case of 3D-Games [3]. The access pattern must be predictable so we can know which data to prefetch at all. The run-time of the program must be large so that the initial latency of memory can be hidden. For example, if memory latency is 1,000,000 cycles and the runtime of the program given a perfect cache is only 100,000 cycles, prefetching will be of little or no benefit. This problem applies more to applications like JPEG than to MPEG-like applications which are tied to a notion of time. Finally, the memory bandwidth must be able to scale because otherwise even perfect prefetching will not be able to keep up with the processor.

5 Future Work

In the future this work could be extended by looking into a larger variety of multimedia applications. Computer games might be an interesting avenue to explore since there is some evidence that they exhibit less memory locality than most other multimedia applications [4].

Another interesting question that remains to be answers is to ask how well prefetching would continue to hide the memory bottleneck if the application memory access patterns were less spatially local. Although previous literature has found that multimedia application are primarily of very small working sets [4], there are several applications that involve complex global interaction between data, such as image segmentation or shape from shading computer vision algorithms.

Another possible avenue for exploration is the impact of I/O on multimedia performance, in the paper we demonstrated that memory performance will not necessarily lead to the obsolescence of multimedia instruction sets, a similar study could look at the impact of network performance or disk latency.

Bibliography

[1] IA-32 Intel Architecture Software Developers Manual (by Intel Corporation)

[2] R. Bhargava et al.: Evaluating MMX Technology Using DSP and Multimedia Applications, Presented at the 1998 ACM/IEEE International Symposium on Microarchitecture

[3] N. Slingerland et al.: Multimedia Instruction Sets for General Purpose Microprocessors: A Survey, Report UCB/CSD-00-1124, University of California at Berkeley, 2000

[4] N. Slingerland et al.: Cache performance for Multimedia Applications, Report UCB/CSD-00-1123, University of California at Berkeley, 2000

[5] N. Slingerland et al.: Measuring the Performance of Multimedia Instruction Sets, Report UCB/CSD-00-1125, University of California at Berkeley, 2000

[6] P. Ranganathan et al.: Performance of Image and Video Processing with General-Purpose Processors and Media ISA Extensions, Proceedings of the 26^th International Symposium on Computer Architecture, 1999

[7] O. Lempel et al.: Intel's MMX Technology - A New Instruction Set Extension, Proceedings of COMPCON, 1997

[8] K. Diefendorff: Pentium III = Pentium II + SSE, Microprocessor Report, Volume 13, Number 3, 1999

[9] D. Zucker et al.: Hardware and Software Cache Prefetching Techniques for MPEG Benchmarks, IEEE Transactions on Circuits and Systems for Video Technology, Volume 10, Number 5, 2000

[10] M. Nelson: The Data Compression Book, M&T Publishing, 1991

[11] D. Talla et al.: Execution Characteristics of Multimedia Applications on a Pentium II Processor, Proceedings of 19th IEEE International Performance, Computing, and Communications Conference (IPCCC), 2000