(a.) For the following configuration space, draw the visibility graph
and the Voronoi diagram (using the L2 metric).
(b.) For each method, highlight the path the a robot would take assuming it
had full knowledge of the world.
(c.) Comment on the significant features of each path and explain why they
are different.
(d.) Given that the configuration space was two dimensional, how many degrees
of freedom does the robot have?

Visibility graph

Voronoi Diagram
Problem #2 (30 points)
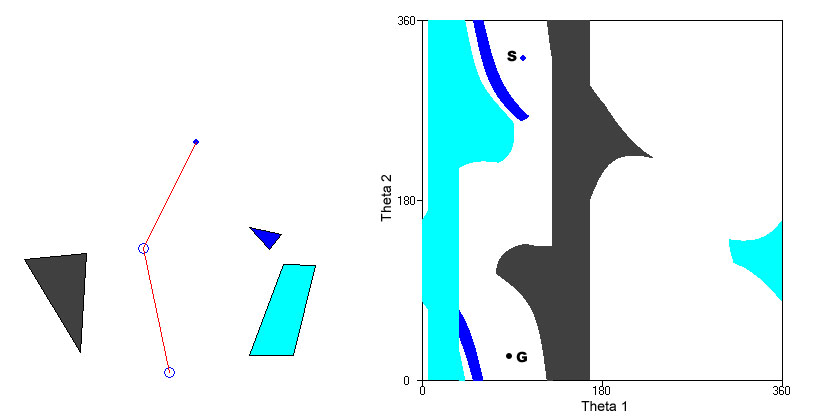
(a.) Given the following workspace (with robot shown at start configuration) and configuration space, use the Wavefront planner to find a path in configuration space from the start configuration to the goal configuration. You may use any metric you want, but be sure to state which you are using. Draw the path on the figure. Note: Theta 1 is the first joint angle and Theta 2 is the second joint angle. The black dot is the end effector, and the joints have no joint limits.
(b.) Draw in the workspace five intermediate configurations between the start and goal configurations, and show their location in the configuration space. (We have provided extra copies of the workspace and configuration space)


Problem #3 (10 points)
In the motion planning lab, some groups used eight-point connectivity when
growing their wave front, i.e., their wave front expanded according to the
generator  as opposed to four-point connectivity,
i.e., a wavefront expanded according to the generator
as opposed to four-point connectivity,
i.e., a wavefront expanded according to the generator  .
.
(a.) Which wavefront generator gives rise to the shortest path in the L1 metric
and why?
(b.) Why does the other not give rise to the shortest path in the L1
metric?
(c.) Does the other generator give rise to the shortest path with the L2 metric?
Why?
Problem #4 (15 points)
(a.) Given the following input signal, match each mask with its corresponding convolved output.
[-1 -1 -1 -1 1 1 1 1 ]:___________ [-1 -1 1 1]:___________ [-1 1]:____________
(b.) Match each mask to its description (draw lines from the mask to description)
|
Mask
|
Description
|
|---|---|
| 1 1 1 0 0 0 -1 -1 -1 1 0 -1 1 0 -1 1 0 -1 0 1 0 1 -4 1 0 1 0 |
horizontal edge detector vertical edge detector Laplacian detector |