Midterm
24-354 General Robotics
Fall-02. Prof. Howie Choset
· You have 1 hour and 15 minutes to complete the exam.
· Please write all answers either on the exam or in a blue book
· You must attempt all five problems
· Good Luck
Problem #1 (25 points)
(a.) (10 points) For the following configuration space, draw a
trapezoidal decomposition and a Boustrophedon decomposition.
(b.) (10 points) For each method, superimpose the adjacency graph on your
drawing.
(c.) (5 points) If you were to use the decomposition to determine a coverage
path, comment on the significant features of each path and explain why they are
different.
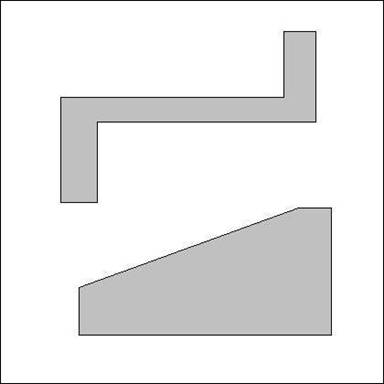
Trapeziodal
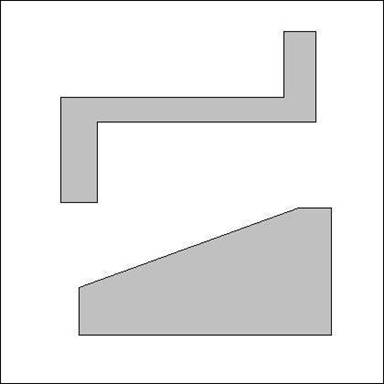
Boustrophedon
Spare for work
Problem #2 (25 points)
(a.) (15 points) Given the following workspace (with robot shown at start configuration) and configuration space, use the Wavefront planner to find a path in configuration space from the start configuration to the goal configuration, subject to no joint limits on Ө1 but Ө2 having limits of 0<Ө2<359.9. Draw the path on the figure. Note: Ө1 is the first joint angle, and Ө2 is the second joint angle.
(b.) (10 points) Draw five intermediate configurations between the start and goal configurations, and show their location in the configuration space.

Problem #3 (20 points)
(a.) (10 points) A mobile robot traveling in a plane typically has a three-dimensional workspace defined by R2 x S1; however, when using the wavefront planner for lab 5, you planned in a two-dimensional array. Why was this allowable?
(b.) (10 points) Given the pentagonal obstacle shown below and the four numbered robot shapes, match each robot shape with the lettered configuration space obstacle for the robot in the configurations shown.
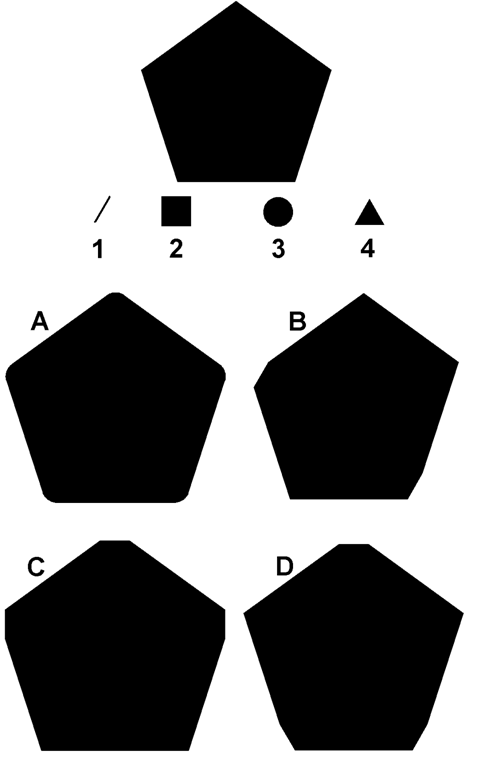
1.)______ 2.)______ 3.)______ 4.)______
Problem #4 (10 points)
(a.) Describe how one of the labs which you completed fits into the paradigm of Sense>Plan>Act.
Problem #5 (20 points)
Given a binary image (black=1 and white=0) of an object, we wish to write a program that will be able to return the number of ‘holes’ that exist in the object. For example, the object in the image below has 3 holes.

We already have written a function, called ‘fill’, which is outlined below:
void fill(char* image, int x, int y, int replace_value, int color)
The function ‘fill’ takes the pointer to an image, an x-y location, and a replace_value which we would like to replace in the image. The function then replaces all of the pixels of replace_value which are contained in the same connected blob as the location x,y with the value color.
Write, in a standard programming language or in
pseudo-code form, a function which, when passed an image, returns the number of
holes in the object of that image.