Logical and Classical Planning Agents

Introduction

In this project, you will implement two different planning frameworks. In the first, your Pacman agent will logically plan his way to the goal. You will write software that generates the logical sentences describing moving around the board and eating food. You will encode initial states and goals and use logical inference to find action sequences that are consistent with these. In the second framework, your Pacman agent will use GraphPlan to find its way to the goal. You will again encode initial and goal states, and you will write the action operators that GraphPlan will use to move and eat its way towards its goal.

These diagrams outline the different steps of the propositional logic and classical planning processes. Notice that the process is the same but the representation of states and actions are different.

As in previous programming assignments, this assignment includes an autograder for you to grade your answers on your machine. This can be run with the command:

python36 autograder.py

See the autograder tutorial in Project 0 for more information about using the autograder.

The code for this project consists of several Python files, some of which you will need to read and understand in order to complete the assignment, and some of which you can ignore. You can download all the code and supporting files as a zip archive.

Files you will edit

Files you might want to look at

Files you will not edit

Files to Edit and Submit: You will fill in portions of logicPlan.py and graphPlan.py during the assignment. You should submit these files with your code and comments. Please do not change the other files in this distribution or submit any of our original files other than these files.

Evaluation: Your code will be autograded for technical correctness. Please do not change the names of any provided functions or classes within the code, or you will wreak havoc on the autograder. However, the correctness of your implementation -- not the autograder's judgements -- will be the final judge of your score. If necessary, we will review and grade assignments individually to ensure that you receive due credit for your work.

Academic Dishonesty: We will be checking your code against other submissions in the class for logical redundancy. If you copy someone else's code and submit it with minor changes, we will know. These cheat detectors are quite hard to fool, so please don't try. We trust you all to submit your own work only; please don't let us down. If you do, we will pursue the strongest consequences available to us.

Getting Help: You are not alone! If you find yourself stuck on something, contact the course staff for help. Office hours, section, and the discussion forum are there for your support; please use them. If you can't make our office hours, let us know and we will schedule more. We want these projects to be rewarding and instructional, not frustrating and demoralizing. But, we don't know when or how to help unless you ask.

Discussion: Please be careful not to post spoilers.

The Expr Class

In the first part of this project, you will be working with the Expr class defined in logic.py to build propositional logic sentences. An Expr object is implemented as a tree with logical operators (\(\land, \lor, \neg, \Rightarrow, \Leftrightarrow\)) at each node and with literals (\(A, B, C\)) at the leaves. The sentence

\[ (A \land B) \Leftrightarrow (\neg C \lor D) \]

would be represented as the tree

To instantiate a symbol named 'A', call the constructor like this:

A = Expr('A')

The Expr class allows you to use Python operators to build up these expressions. The following are the available Python operators and their meanings:

• ~A: \(\neg A\)
• A & B: \(A \land B\)
• A | B: \(A \lor B\)
• A >> B: \(A \Rightarrow B\)
• A % B: \(A \Leftrightarrow B\)

So to build the expression \(A \land B\), you would type this:

A = Expr('A')

B = Expr('B')

a_and_b = A & B

(Note that A to the left of the assignment operator in that example is just a Python variable name, i.e. symbol1 = Expr('A') would have worked just as well.)

One last important thing to note is that typing in A & B & C will give the expression ((A & B) & C). If instead you want (A & B & C), as you will for these problems, use logic.conjoin, which takes a list of expressions as input and returns one expression that is the conjunction of all the inputs. The & operator in Python is a binary operator and builds an unbalanced binary tree if you chain it several times, whereas conjoin builds a tree that is one level deep with all the inputs extending directly from the & operator at the root. logic.disjoin is similarly defined for |. The autograder for Question 1 will require that you use logic.conjoin and logic.disjoin wherever you could otherwise chain several & operators or several | operators. If you keep with this convention for later problems, it will help with debugging because you will get more readable expressions.

There is additional, more detailed documentation for the Expr class in logic.py.

Tips

• When creating a symbol with Expr, it must start with an upper case character. You will get non-obvious errors later if you don't follow this convention.
• Be careful creating and combining Expr instances. For example, if you intend to do x = Expr('A')&Expr('B'), you don't want to accidentally type x = Expr('A&B'). The former will be a logical expression of the symbol 'A' and the symbol 'B', while the latter will be a single symbol (Expr) named 'A&B'.

SAT Solver Setup

A SAT (satisfiability) solver takes a logic expression which encodes the rules of the world and returns a model (true and false assignments to logic symbols) that satisfies that expression if such a model exists. To efficiently find a possible model from an expression, we take advantage of the pycosat module, which is a python wrapper around the picoSAT library.

Unfortunately, this requires installing this module/library on each machine.

To install this software in the Andrew Linux servers:

1. ssh -Y @unix.andrew.cmu.edu
2. Install pycosat: pip install --user pycosat. There should be no errors.

To install this software on your own machine, please follow these steps:

1. Install pip3 (if you don't have it installed on your system already). See pip installation instructions (Note: may requires super-user (sudo) permissions)
2. Install pycosat: On command line run: pip3 install pycosat. (Note: you may need to run: sudo pip3 install pycosat). There should be no errors.

Testing pycosat installation:

After unzipping the project code and changing to the project code directory, run:

python36 pycosat_test.py

This should output:

[1, -2, -3, -4, 5].

Please let us know if you have issues with this setup. This is critical to completing the project, and we don't want you to spend your time fighting with this installation process.

Question 1 (2 points): Logic Warm-up

This question will give you practice working with the logic. Expr data type used in the project to represent propositional logic sentences.

Fill in the functions sentence1(), sentence2(), and sentence3() in the file logicPlan.py, which ask you to create specific logic.Expr instances.

For sentence1(), create one logic.Expr instance that represents that the following three sentences are true. Do not do any logical simplification, just put them in in this form in this order.

\[ A \lor B \]

\[ \neg A \Leftrightarrow \neg B \lor C \]

\[ \neg A \lor \neg B \lor C \]

For sentence2(), create one logic.Expr instance that represents that the following four sentences are true. Again, do not do any logical simplification, just put them in in this form in this order.

\[ C \Leftrightarrow B \lor D \]

\[ A \Rightarrow \neg B \land \neg D \]

\[ \neg (B \land \neg C) \Rightarrow A \]

\[ \neg D \Rightarrow C \]

For the planning problems later in the project, we will have symbols with names like \(P[3, 4, 2]\) which represent that Pacman is at position \((3, 4)\) at time \(2\), and we will use them in logic expressions like the above in place of \(A, B, C, D\). The logic.PropSymbolExpr constructor is a useful tool for creating symbols like \(P[3, 4, 2]\) that have numerical information encoded in their name (for this, you would type PropSymbolExpr('P', 3, 4, 2)).

Using the logic.PropSymbolExpr constructor, create symbols WumpusAlive[0], WumpusAlive[1], WumpusBorn[0], and WumpusKilled[0], and create one logic.Expr instance which encodes the following three English sentences as propositional logic in this order without any simplification:

The Wumpus is alive at time 1 if and only if he was alive at time 0 and he was not killed at time 0 or he was not alive at time 0 and he was born at time 0.

At time 0, the Wumpus cannot both be alive and be born.

The Wumpus is born at time 0.

Are sentence1(), sentence2(), and sentence3() satisfiable? If so, try to find a satisfying assignment. (This is not graded, but is a good self-check to make sure you understand what's happening here.)

Before you continue, try instantiating a small sentence, e.g. \(A \land B \implies C\) and call logic.to_cnf on it. Inspect the output and make sure you understand it (refer to AIMA section 7.5.2 for details on the algorithm logic.to_cnf implements).

Now, implement a small function findModel(sentence), which uses logic.to_cnf to convert the input sentence into Conjunctive Normal Form (the form required by the SAT solver), then passes it to the SAT solver using logic.pycoSAT to find a satisfying assignment to the symbols in sentence, i.e., a model. A model is a dictionary of the symbols in your expression and a corresponding assignment of True or False. You can test your code on sentence1(), sentence2(), and sentence3() by opening an interactive session in Python and running findModel(sentence1()) and similar queries for the other two. Do they match what you thought?

To test and debug your code run:

python36 autograder.py -q q1

Question 2 (2 points): Logic Workout

Implement the following three logic expressions in logicPlan.py:

• atLeastOne(literals): Return a single expression (Expr) in CNF that is true only if at least one expression in the input list is true. Each input expression will be a literal.
• atMostOne(literals): Return a single expression (Expr) in CNF that is true only if at most one expression in the input list is true. Each input expression will be a literal.
• exactlyOne(literals): Return a single expression (Expr) in CNF that is true only if exactly one expression in the input list is true. Each input expression will be a literal.

The function definitions have been started for you in logicPlan.py. Do not change the function signature.

Each of these methods takes a list of logic.Expr literals and returns a single logic.Expr expression that represents the appropriate logical relationship between the expressions in the input list. An additional requirement is that the returned Expr must be in CNF (conjunctive normal form). You may NOT use the logic.to_cnf function in your method implementations (or any of the helper functions logic.eliminate_implications, logic.move_not_inwards, and logic.distribute_and_over_or).

When implementing your planning agents in the later questions, you will not have to worry about CNF until right before sending your expression to the SAT solver (at which point you can use findModelfrom question 1).logic.to_cnf implements the algorithm from section 7.5 in AIMA. However, on certain worst-case inputs, the direct implementation of this algorithm can result in an exponentially sized sentences. In fact, a certain non-CNF implementation of one of these three functions is one such worst case. So if you find yourself needing the functionality of atLeastOne, atMostOne, or exactlyOne for a later question, make sure to use the functions you've already implemented here to avoid accidentally coming up with that non-CNF alternative and passing it to logic.to_cnf. If you do this, your code will be so slow that you can't even solve a 3x3 maze with no walls.

You may utilize the logic.pl_true function to test the output of your expressions. pl_true takes an expression and a model and returns True if and only if the expression is true given the model.

To test and debug your code run:

python36 autograder.py -q q2

Question 3 (1 point): Extract the Solution

In future questions you will be assembling logic expressions to pass to a SAT solver. The SAT solver returns a model that will cause the logic expressions to be true. In the Pacman world, we need to convert this model into a specific sequence of actions ('North', 'South', 'East', 'West') that will lead Pacman to the goal.

Implement the following function in logicPlan.py:

• extractActionSequence(model, actions): Returns an ordered sequence of action strings based on the given model.

The function definition has been started for you in logicPlan.py. Do not change the function signature.

A model is a dictionary of the symbols in your expression and a corresponding assignment of True or False. The keys in the model dictionary will be symbols in the form of a logic.PropSymbolExpr. The model will contain assignments of True/False to many different symbols used in the Pacman world. Within the many symbols in the model, some of them will be action symbols. Each action will have a different symbol for each time point. For example 'East[3]', represents the symbol for taking the action 'East' at time t=3. This method must find the actions symbols that are true in the model and return an ordered list of action strings. The variable actions contain all of the possible actions that could be taken at any time point. Each action symbol will follow the very specific format of action_string[t] where action_string is one of actions and t will range from 0 to max_time - 1.

For your convenience, we've included the method parseExpr which will do the regex parsing of a symbol in one of these formats for you. Look at that function in logic.py to read its output format.

To test and debug your code run:

python36 autograder.py -q q3

Example test code:

import logicPlan
from logic import PropSymbolExpr as PSE
model = {PSE("North",2):True, PSE("P",3,4,1):True, PSE("P",3,3,1):False,
         PSE("West",0):True, PSE("GhostScary"):True, PSE("West",2):False, 
         PSE("South",1):True, PSE("East",0):False}
actions = ['North', 'South', 'East', 'West']
plan = logicPlan.extractActionSequence(model, actions)
print plan

The above should print: ['West', 'South', 'North']

Question 4 (2 points): Pacman Successor State Axioms

Implement the following function in logicPlan.py:

• pacmanSuccessorStateAxioms(x, y, t, walls_grid)

This function takes in a position as x and y, a time t, and walls_grid, which is a game.Grid object representing where the walls on the board are (refer to the Grid class for documentation). The function should return the successor state axiom for Pacman's position being (x,y) at time t.

We will use 'P' as the string for Pacman's location. That is, the symbol that "Pacman is at position (3, 4) at time 2" should be P[3, 4, 2]. In your code, you should use the constant pacman_str to represent this (so logic.PropSymbolExpr(pacman_str, 3, 4, 2) will return P[3, 4, 2]).

Remember that the general formula for successor state axioms is

\[ X[t] \Leftrightarrow (X[t-1] \land \text{Nothing caused \(\neg X\) at time \(t-1\)}) \lor (\neg X[t-1] \land \text{Something caused \(X\) at time \(t-1\)}) \]

However, in this problem, the 'Stop' action is not allowed, so Pacman's position will always change. This gives instead the formula

\[ P[x, y, t] \Leftrightarrow \text{Pacman was at an adjacent square at \(t-1\)} \land \text{Pacman moved into \((x,y)\) at \(t-1\)} \]

Your job is to break this down into the possibilities for how Pacman could've moved into this square at this time.

Note: the possible adjacent squares Pacman could have previously been in depends on where the walls are.

To test and debug your code run:

python36 autograder.py -q q4

Hint: If you are struggling, try re-reading AIMA chapter 7.7, "Agents Based on Propositional Logic."

Question 5 (5 points): Solve the Maze

Pacman is trying to find the end of the maze (the goal position). Implement the following method using propositional logic to plan Pacman's sequence of actions leading him to the goal:

• positionLogicPlan(problem): Given an instance of logicPlan.PlanningProblem, returns a sequence of action strings for the Pacman agent to execute.

You will not be implementing a search algorithm, but creating expressions that represent the Pacman game logic at all possible positions at each time step.

To build these expressions, think about what you know about the problem: where Pacman starts, the logical axioms that move him to the next state, the actions Pacman can take, and the goal state. Which can be formulated as logical expressions? Which of these have strict requirements on how many are true at each time step? Think about whether the axioms be applied to every state or only some states at every time step.

To find a model that satisfies your logical expression, you should call findModel from question 1.

You should gradually increase the max time step until you find a model that satisfies all the expressions from time 0 to the max time step.

We will not test your code on any layouts that require more than 50 time steps.

Your function needs ultimately to return a list of actions that will lead the agent from the start to the goal. These actions all have to be legal moves (valid directions, no moving through walls).

Test your code on smaller mazes using:

python36 pacman.py -l maze2x2 -p LogicAgent -a fn=plp

python36 pacman.py -l tinyMaze -p LogicAgent -a fn=plp

To test and debug your code run:

python36 autograder.py -q q5

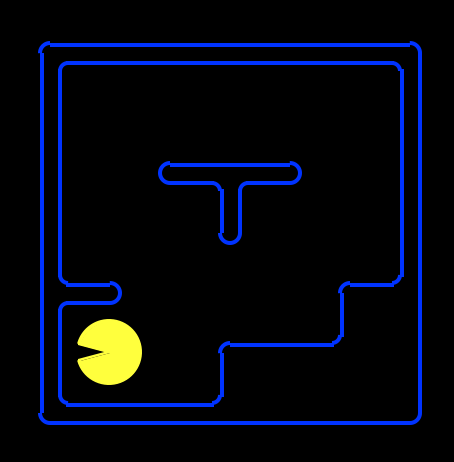
Note that with the way we have Pacman's grid laid out, the leftmost, bottommost space occupiable by Pacman (assuming there isn't a wall there) is (1, 1), as shown below.

Hint: You already implemented the successor state axioms which detail how Pacman moves. What's missing is where he starts, where his goal is, and that he must take an action every turn.

Hint: Remember to use atLeastOne, atMostOne, and exactlyOne from question 2 if you ever need that functionality.

Hint: If you are struggling, try re-reading AIMA chapter 7.7, "Agents Based on Propositional Logic."

Debug hint: If you're finding a length-0 or a length-1 solution: is it enough to simply have axioms for where Pacman is? What's to prevent him from also being in other places?

Debug hint: Coming up with some of these plans can take a long time. It's useful to have a print statement in your main loop so you can monitor your progress while it's computing.

Question 6 (4 points): Eat the Food

Pacman is trying to eat all of the food on the board. This is the same problem setup as the search problems in Project 1. Implement the following method using propositional logic to plan Pacman's sequence of actions leading him to the goal.

• foodLogicPlan(problem): Given an instance of logicPlan.PlanningProblem, returns a sequence of action strings for the Pacman agent to execute.

This question has the same general format as question 5. The notes and hints from question 5 apply to this question as well. You are responsible for implementing whichever successor state axioms are necessary that were not implemented in previous questions.

Test your code using:

python36 pacman.py -l testSearch -p LogicAgent -a fn=flp,prob=FoodPlanningProblem

We will not test your code on any layouts that require more than 50 time steps.

To test and debug your code run:

python36 autograder.py -q q6

GraphPlan Setup

You have implemented a framework for Pacman to find its way to the goal using logic-based planning. Now you will implement a framework for Pacman to find the same goals using the classical planning algorithm GraphPlan. Similar to LogicPlan, you will represent Pacman at locations in his maze. Each part of Pacman's state must be implemented as boolean propositions, just like your implementation of LogicPlan. However, unlike LogicPlan, you will not explicitly represent time. Instead, the GraphPlan solver uses your implementation of actions (operators) which explicitly add and delete propositions in the state to enumerate the possible state propositions at each level of the planning graph and those levels represent time. While LogicPlan searches for a satisfying set of variables to plan a path, GraphPlan will search for the first level when all goal propositions are present and not mutually exclusive (i.e., all goals can be met at the same time).

Our GraphPlan solver represents the world as Instances, Variables, Propositions, and Operators.

For an example of a GraphPlanProblem formulation, look at rocket.py. You can run this using:

python36 rocket.py

Instances are all of the literals and constants in the model. Each Instance has a Type. In the rocket example, London and Paris are Instances of Type PLACE; the rocket is an Instance of Type ROCKET.

# Types
ROCKET = 'Rocket'
PLACE = 'Place'

# Instances
i_rocket = Instance('rocket', ROCKET)
i_london = Instance('london', PLACE)
i_paris = Instance('paris', PLACE)

(You do not have to follow the i_ naming convention, but we have done so here for clarity.)

Because the planner deals only in Instances, any integers you want to use must be declared as INT types. The rocket example includes those as well. You will be responsible for creating any Instances you use in your implementation.

Variables can take the value of any Instance of the same Type. For example, in the rocket problem we created a variable

v_from = Variable('from', PLACE)

which can take the value of any possible place that we have created. Note that the string 'from' must be unique in the environment. You will use these variables in your operators.

Propositions are boolean descriptors of the environment and contain a string descriptor, and either one instance that satisfies the descriptor or multiple instances that have a relationship satisfying that descriptor.

We write Proposition('boolean_desc', instance/variable1, instance/variable2) if instance1/variable1 and instance2/variable2 are related by boolean_desc, and we write ~Proposition('boolean_desc', instance1/variable1, instance2/variable2) if the relationship is false. For example, if the rocket is starting at the instance for London then it is 'at' London and not 'at' Paris.

Proposition('at', i_rocket, i_london)
~Proposition('at', i_rocket, i_paris)

Note: the list [Proposition('at', i_rocket, i_london), ~Proposition('at', i_rocket, i_paris)] represents the conjuction of those propositions.

One special proposition that GraphPlan provides, SUM, checks whether two integer instances sum to the third.

i1 = Instance(1, INT)
i2 = Instance(2, INT)
Proposition(SUM, i1, i1, i2)

SUM is defined for you in graphplanUtils.py and does not need to be added explicitly to the initial state but can still be used in operators. The rocket example uses SUM to compute the amount of fuel left.

Operators contain lists of preconditions, add effects, and delete effects which are all composed of propositions. Operators will test the current state propositions to determine whether all the preconditions are true by matching available instances and/or variables, and then add and delete state propositions to update the state.

i_rocket = Instance('rocket', ROCKET)
i_london = Instance('london', PLACE)

v_fuel_start = Variable('start fuel', INT)
v_fuel_end = Variable('end fuel', INT)
v_from = Variable('from', PLACE)
v_to = Variable('to', PLACE)

o_move = Operator('move',          # The name of the action
                  # Preconditions
                  [Proposition(NOT_EQUAL, v_from, v_to),
                   Proposition('at', i_rocket, v_from),
                   Proposition('fuel_at', v_fuel_start),
                   Proposition(LESS_THAN, i_ints[0], v_fuel_start),
                   Proposition(SUM, i_ints[1], v_fuel_end, v_fuel_start)],
                  
                  # Add effects
                  [Proposition('at', i_rocket, v_to),
                   Proposition('fuel_at', v_fuel_end)],

                  # Delete effects
                  [Proposition('at', i_rocket, v_from),
                   Proposition('fuel_at', v_fuel_start)])

In order to perform the move operation, the source must not equal the destination; the rocket must be at the source; the rocket must have v_fuel_start units of fuel such that v_fuel_start > 0 and v_fuel_end + 1 = v_fuel_start.

After moving, the rocket is now at the destination and has v_fuel_end units of fuel. It is no longer at the source, and the no longer has v_fuel_start units of fuel.

Note: If the proposition must match the state exactly in the precondition or effects, use an instance. If any instance can be matched, use a variable of the correct type. For example, we can find the sum of any number and 2 using Proposition(SUM, vint1, i2, vint2) assuming that vint1 and vint2 are declared as Variables of type INT and i2 = Instance(2, INT) as above. In this case, any variables that satisfy the +2 requirement could be matched.

If you need to match two propositions on the same instance, the variable name should be the same for both propositions. For example, in order to find three numbers that count by 2's, we could write [Proposition(SUM, vint1, i2, vint2), Proposition(SUM, vint2, i2, vint3)].

The GraphPlan solver would use the same integer in place of both vint2. Note again that the variables must be defined before an operator can use them and that you should not replicate integer instances. Also note that ~Proposition and Proposition are not mutually exclusive in our implementation. You must explicitly delete propositions in your operators that can no longer be matched.

Question 7 (5 points): Solve the Maze Using GraphPlan

Pacman is trying to find the end of the maze, again. This is the same as Q5 except you are asked to use graph planning instead of propositional logic. Implement the following method by modelling the problem as a graph planning problem to plan Pacman's sequence of actions leading him to the goal:

• positionGraphPlan(problem): Given an instance of graphPlan.PlanningProblem, returns a sequence of action strings for the Pacman agent to execute.

You should think about the axioms defined in Q4, and define operators [o_west, o_east, o_north, o_south] (and necessary variables) that allow those axioms to be achieved.

We have provided you with the 4 types - PACMAN, OPEN, WALL, and FOOD - in addition to INT which is defined in graphPlanUtils.py. It is up to you to decide which are necessary for the problems.

If you'd like to test your code before implementing all 4 operators, you can run

python36 pacman.py -p GraphPlanAgent -a fn=positionGraphPlan,prob=PositionPlanningProblem -l <LAYOUT>

With <LAYOUT> being one of:

• mazeDown: only requires o_south to solve.
• mazeLshape: only requires o_south and o_west to solve.
• mazeUshape: only requires o_south, o_west, and o_north to solve.

Test your code with all 4 operators using:

python36 pacman.py -p GraphPlanAgent -a fn=positionGraphPlan,prob=PositionPlanningProblem -l tinyMaze

And for a challenge, try

python36 pacman.py -p GraphPlanAgent -a fn=positionGraphPlan,prob=PositionPlanningProblem -l smallModifiedMaze

Your function needs to return a list of actions ('North', 'South', 'East', 'West') that Pacman can use to go from the start to the goal. These actions all have to be legal moves (valid directions, no moving through walls). We have provided you with example code of generating and solving a GraphPlan problem in rocket.py. You will have to translate the GraphPlan actions into Pacman actions to return. To get the string names of a GraphPlan ActionNodes in the returned solution, you can use action.print_name().

To test and debug your code run:

python36 autograder.py -q q7

Question 8 (4 points): Eat the Food Using GraphPlan

Pacman is trying to eat all of the food on the board, again. This is the same as Q6 except you are asked to use graph planning instead of propositional logic. Implement the following method by modelling the problem as a graph planning problem to plan Pacman's sequence of actions leading him to the goal.

• foodGraphPlan(problem): Given an instance of graphPlan.PlanningProblem, returns a sequence of action strings for the Pacman agent to execute.

Test your code on a smaller layout using:

python36 pacman.py -p GraphPlanAgent -a fn=foodGraphPlan,prob=FoodPlanningProblem -l tinyMaze

If you want to test your code on increasingly more complex layouts, run

python36 pacman.py -p GraphPlanAgent -a fn=foodGraphPlan,prob=FoodPlanningProblem -l <LAYOUT>

With <LAYOUT> being one of mazeSearch1 or mazeSearch2.

You should be using move actions as in Q7 and adding an operator o_eat to eat the food. Think about when food can be eaten and look at the start state and goal state to determine which propositions you should modify. However, make sure that the action list returned does not include the eat action (eating food is implied in that model).

To test and debug your code run:

python36 autograder.py -q q8

Submission

python36 autograder.py

python36 autograder.py -q q3