Homework 3

In this homework, you will be computing the Fourier series expansions of some simple signals.

I. Square Wave

A square can be written in multiple ways. You can use one of the two mathematical expressions below or write your own \[ x(t) = \left\{ \begin{array}{lc} sgn(sin(t)), & t \leq T \\ 0, & elsewhere \end{array} \right. \] where T is the period of the sine \[or\] \[ x(t) = \left\{ \begin{array}{lc} +1 ,& 0 \leq t < \frac{T}{2} \\ -1 , & \frac{T}{2} \leq t \leq T \\ 0 , & elsewhere \\ \end{array} \right. \]

II. Triangle Wave

Do the same for the Triangle Wave. \[ x(t) = \left\{ \begin{array}{lc} \int sgn(sin(t)), & t \leq T \\ 0, & elsewhere \end{array} \right. \]

Hint: The Triangle wave is the integral of the square wave

III. Amplitude modulated Sine wave

Here, the envelope of a low frequency sine is applied to the amplitude of a high frequency sinusoidal carrier \[ x(t) = a(t) * sin(\omega t) \] \[ where\ a(t) = \left\{ \begin{array}{lc} sin(\omega_{1}t), & t \leq T \\ 0, & elsewhere \end{array} \right. \] \[ and\ \omega_{1} \ll \omega \]

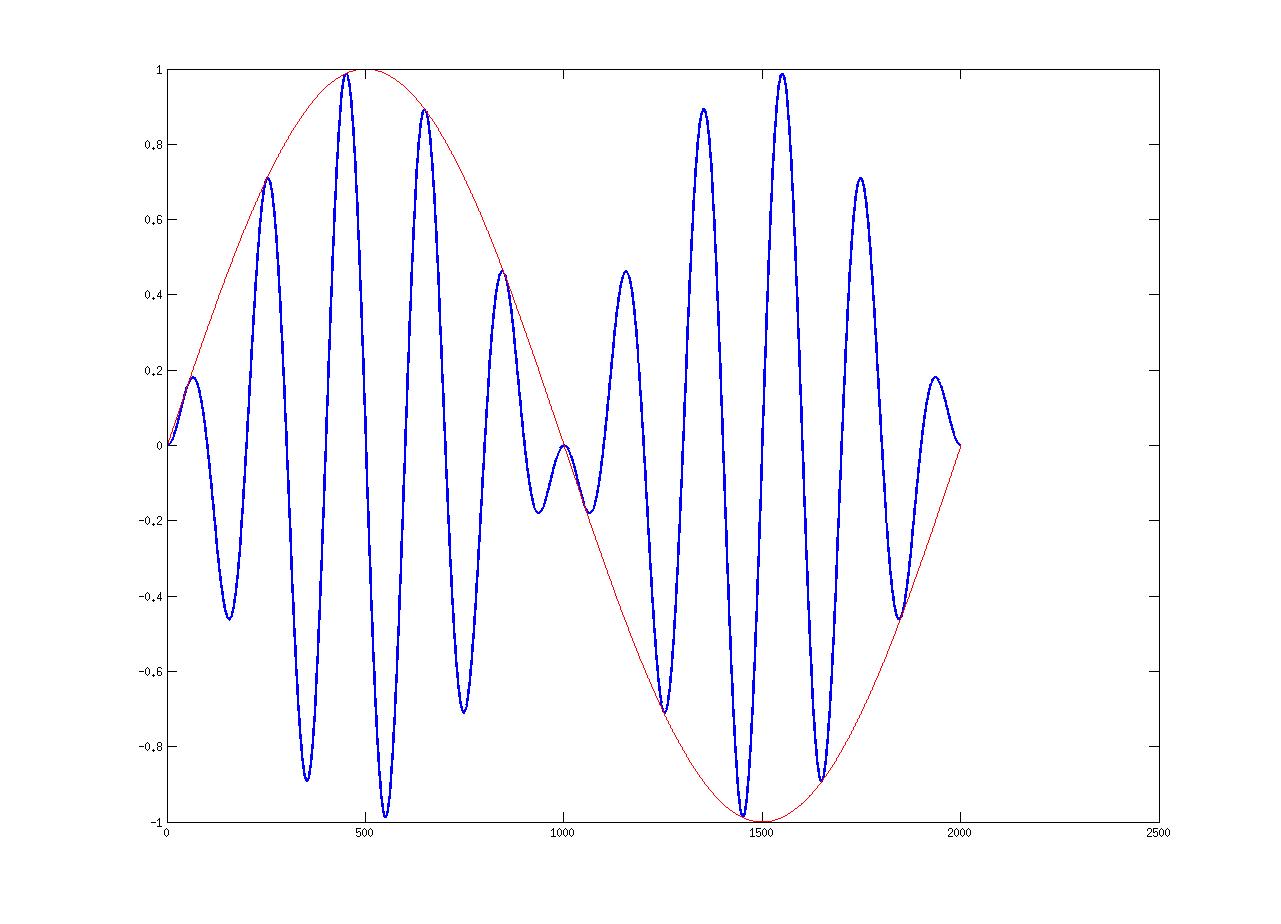
The red signal is the original low frequency sine and the blue signal is the amplitude modulated sine

IV. Gaussian

Compute the Fourier Transform of a Gaussian. To make things simpler, let's assume that the Gaussian is zero mean and has a variance of 1: \[ f(t) = \frac{1}{\sqrt{2\pi}} e^{t^{2}} \]

V. Triangle

Compute the Fourier Transform of a triangle of width T centered at 0. \[ x(t) = \left\{ \begin{array}{lc} \ \frac{|T|}{2}-t, & t \leq \frac{|T|}{2} \\ 0, & elsewhere \end{array} \right. \]

You can use any properties of the Fourier transform such as the integral property or the convolution property.

VI. Triangular Wave again

Compute the Fourier transform of a triangular wave with each triangle of width T. Make use of the result of V. and the fact that a triangular wave can be composed by convolving a Triangle with a pulse train. You also already know the Fourier transform of a pulse train.