
Next: Bibliography
Up: Statistical Techniques
Previous: Spearman's Rank Correlation Test
This tests the significance of the correlation between  series of rank numbers, assigned by
series of rank numbers, assigned by  judges to
judges to 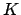 subjects. The
subjects. The  judges give rank numbers to the
judges give rank numbers to the 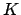 subjects and we compute:
subjects and we compute:
and 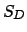 , the sum of squares of the differences between subjects' mean ranks and the overall mean rank. Let:
, the sum of squares of the differences between subjects' mean ranks and the overall mean rank. Let:
The test statistic is:
which follows the 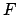 distribution with
distribution with  degrees of freedom.
degrees of freedom.
Derek Long
2003-11-06
![]() series of rank numbers, assigned by
series of rank numbers, assigned by ![]() judges to
judges to ![]() subjects. The
subjects. The ![]() judges give rank numbers to the
judges give rank numbers to the ![]() subjects and we compute:
subjects and we compute: