In all the examples so far, you've seen only a finite number of states,
and hence, a finite number of state transitions, i.e., S and
were finite. I have been able to draw state
transition diagrams for these state machines in their
entirety. For software systems in general we must
deal with an infinite number of states and hence an infinite number
of state transitions. Their state transition diagrams are impossible
to draw out completely (at least in the way I've been drawing them).
The simplest example is an integer counter (which is like a ticking clock), initialized at 0.
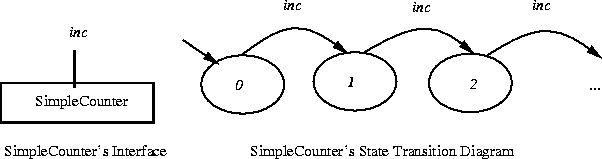
As soon as need to model a system that deals with any domain with an infinite set of values, e.g., integers, then I admit the possibility of an infinite number of states. Can you see now why most programs, let alone software systems, are infinite state machines?
My SimpleCounter example has just one action,
inc. It has an infinite number of state
transitions
because there is an infinite number of states over which the state
transition relation, , is defined--because there is an
infinite number of values that the SimpleCounter can take.
Now, suppose I want to write a description of the state machine using the notation you've seen so far. I would write it something like this:
SimpleCounter = (
).
The problem is what about those two occurrences of
? Here, the pattern is clear and we can probably rely on
sharing the same
intuition as to what goes in those . In general, we need a
way to describe more complex sets.
We would
like to find a way to characterize an infinite set of things
in terms of a finite string of symbols.
Fortunately, predicate logic provides just the notation we need. To characterize the set of all non-negative integers, I can write:
I can even characterize the set of initial states using a predicate:
I've taken care of the first occurrence of , but
what about the second? I can define the state transition relation, , as
a set of triples, (s, a, s'), for which the pair
of states, s, s', satisfies a given predicate.
I can do this for each action in A and then take the union of these
sets.
For example, I can define the set of triples,
(s, a, s'), that inc
contributes to as follows:
where 
, as defined above.
Since my SimpleCounter has only one action, = 
.
In general,
Notice the power of set notation and predicate logic. Using a few
symbols I am able to write out the state transition relation which is
defined on an infinite set of states. The critical thing is that
because I have a finite set of actions, I can define a finite
number of 
, one for each action; in so doing, I am
describing the state transition relation, , which is a
possibly infinite set of state transitions (because I may have to
define it over an infinite number of states).
To be pedantic, I can put this all together and rewrite my description of SimpleCounter as follows:
SimpleCounter = 
.
Technical Aside: The observant reader will notice that I'm using the state name for two purposes: to name the state and to give the value of the SimpleCounter in that state. In the next handout we will refine the structure of states that will allow me to make a distinction between names and values.